Разработка системы классификации инерциальных данных
Development of an inertial data classification systemУДК 004.8 10.05.2018 Выходные сведения: Авторы: Authors: Ключевые слова: Keyword: Аннотация: В данной статье приводится описание работы алгоритма, который благодаря использованию минимального количества данных и выполнению простейших операций позволил бы классифицировать инерциальные данные с минимальным количеством затрат памяти и высокой скоростью выполнения. После разработки алгоритма также было проведено его тестирование и сравнение полученных результатов с его основными популярными аналогами – SVM и k¬-средних. Разработанный алгоритм способен не только стать более эффективным аналогом популярных алгоритмов классификации для решения определенного круга задач, но также может ускорить работу современных нейронных сетей в качестве альтернативы слоям нейронов как составная часть сложных систем классификации, что сделает их работу еще более доступной и дешевой. Annotation: The problem of data classification can appear in a wide list of applications in the field of data analysis – this is because the problem attempts to learn the relationship between a set of feature variables and a target variable. Over the past three decades many data classification methods have been developed, but different types of data require different methods. One of the most frequently categorized data types for solving various tasks is text and numerical data. However, not all methods of data classification are equally popular and effective for solving such problems. This article describes the operation of the algorithm, which could classify inertial data with a minimal amount of memory and high execution speed because of using minimum amount of data and the simplest operations. After development of the algorithm it also has been tested and the results have been compared with its main popular counterparts – SVM and k-means. The developed algorithm is able not only to become a more effective analog of popular classification algorithms for solving a certain range of data mining problems, but it can also speed up the work of modern neural networks as an alternative to neuron layers as an integral part of complex classification systems that will make their work even more accessible and cheaper. Введение Проблема классификации данных является одной из наиболее широко изучаемых в среде сообществ, занимающихся интеллектуальным анализом данных и машинным обучением. Эта проблема была изучена исследователями различных областей в течение нескольких десятилетий. Приложения классификации включают в себя широкий спектр проблемных областей – работа с текстом, мультимедиа-данными, социальными сетями, различными наборами биометрических данных и т.д. Задача классификации данных может возникнуть в самых разнообразных приложениях области анализа данных – это связано с тем, что данная задача пытается изучить взаимосвязь между набором функциональных переменных и целевой переменной. Многие практические проблемы могут быть выражены подобной зависимостью, что обеспечивает широкий диапазон применимости данной модели. Задача классификации может быть сформулирована следующим образом: определение метки класса для произвольного непомеченного объекта на основе обучающей выборки объектов, обладающих соответствующими метками классов (т.е. объектов с известной принадлежностью к классам) [1]. Кроме того, существуют многочисленные вариации данной задачи [2, 3, 4, 5]. В течение последних трех десятилетий были разработаны многие методы классификации – метод опорных векторов (SVM от англ. Support Vector Machine) [6, 7], нейронные сети [8], индукция правил (англ. rule learning) [9], наивный байесовский классификатор (англ. Naive Bayes classifier) [10], метод k ближайших соседей (KNN от англ. k-nearest neighbor algorithm) [11], дерево принятия решений (англ. Decision Tree) [12] и многие другие. Различные типы данных требуют использования разных методов классификации [13]. Это связано с тем, что выбор типа данных часто определяет тип проблемы, решаемый задачей классификации. Одними из наиболее часто подвергающихся классификации типов данных для решения различного круга задач – это текстовые и числовые данные. Однако не все методы классификации одинаково популярны и эффективны для решения подобного рода задач. Некоторые классификаторы на основе логических правил – например, RIPPER [14], были изначально разработаны именно для классификации текстовых данных. Иногда используются нейронные методы и различные линейные классификаторы. К примеру, популярным линейным классификатором, используемым для классификации текста, является метод Роккио [15, 16]. Целью настоящей работы является описание алгоритма, который благодаря использованию минимального количества данных и выполнению простейших операций позволил бы классифицировать данные с минимальным количеством затрат памяти и высокой скоростью выполнения. После разработки алгоритма также было проведено его тестирование и сравнение полученных результатов с его основными популярными аналогами – SVM и k-средних (англ. k-means)[17, 18]. Материалы и методы Материалами исследований предметной области послужили справочные, научные и научно-популярные литературные источники, интернет-ресурсы по соответствующей тематике, а также опубликованные за последние несколько десятилетий научные работы. Среди методов, используемых для достижения целей данной работы, основными являются экспериментальный метод научного исследования и метод моделирования.
Результаты и обсуждение Для написания библиотеки, содержащей исходный код рассматриваемого алгоритма, был использован язык программирования С++. Для визуализации данных и работы алгоритма был использован язык программирования Python версии 3.5.2 с применением библиотеки MathPlotLib. MathPlotLib – свободно распространяемая библиотека на языке Python для визуализации двумерных и трехмерных данных. Интерфейс библиотеки является процедурным, что обеспечивает удобство при работе. При использовании пакета с другими свободно распространяемыми библиотеками Python – NumPy, SciPy и др., можно получить достойную альтернативу MATLAB [19].
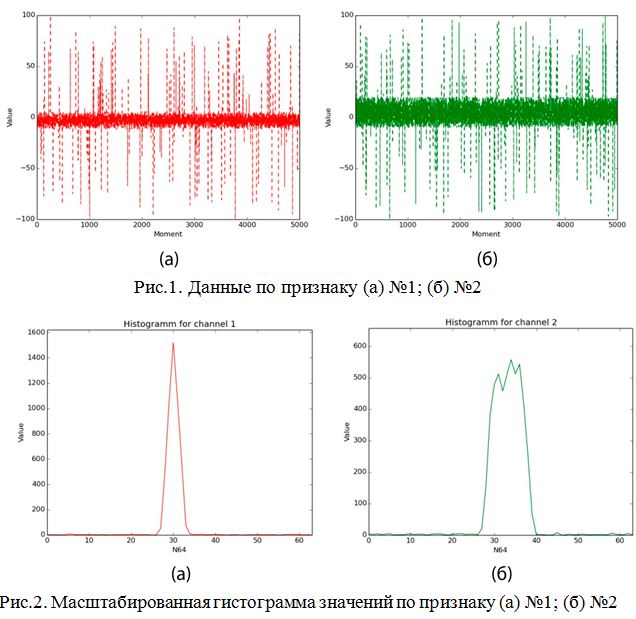
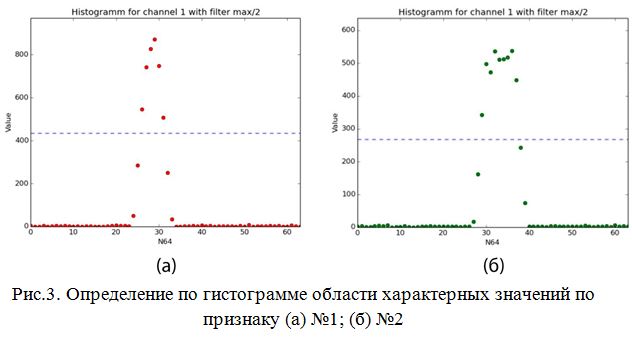
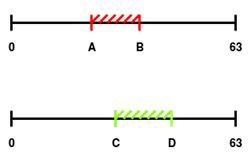
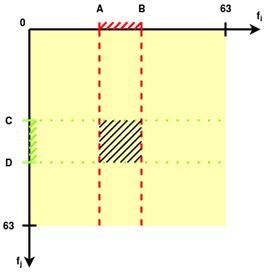
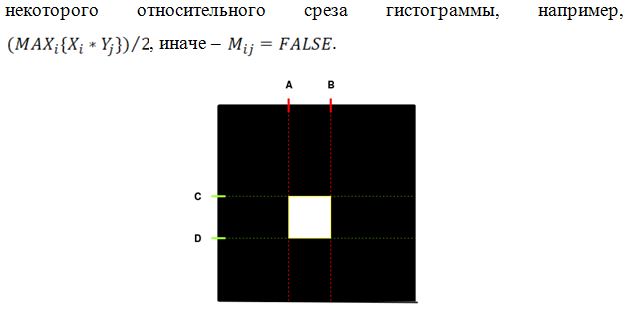
Описание решения Являясь по типу основанным на управлении данными (data-driven), в котором используются различные преобразования данных, из множества которых отбираются самые полезные для составления статистической модели [20], реализуемый алгоритм решает задачу классификации при помощи применения различных функций порождения признаков (features) и отбора из них наиболее полезных для определения класса. Формально действие алгоритма можно описать следующим отношением: где: L – общая выборка, h – относительный срез гистограммы, R – границы области значения признаков, M – множество попарных бинарных матриц, w – множество коэффициентов полезности признаков. В нашем случае для каждого канала рассчитывается коэффициент полезности. Возможно задать количество наиболее полезных каналов при классификации, что позволит сократить количество менее информативно важных вычислений. Иными словами, алгоритм основан на построении характерных статистических моделей для класса. В данном случае характерным считается тот признак, чья область значений является более узкой, поскольку в таком случае вероятность случайного попадания в область уменьшается. Коэффициент полезности рассчитывается как где А – размер всего множества значений величины признака, k – размер области, характерной для данного класса по данному признаку. Например, если получившаяся при обучении область характерных значений признака по классу будет равна всей области значений признака, то любое значение при тестировании будет входить в получившуюся ключевую область. Очевидно, что коэффициент полезности такого признака равен При обучении в каждый момент времени хранится файловый дескриптор, текущее значение, считанное из файла гистограммы значений, т.е. массив Допустим, некий признак принимает значения от 0 до 10000 единиц. У нас имеется класс, для которого величина этого признака принимает в основном значения от 1300 до 1800. В таком случае коэффициент полезности признака составляет 10000 / (1800 — 1300) = 20. Диапазон от 1300 до 1800 будем считать характерным для класса по данному признаку с коэффициентом полезности 20. Чем больше область значений признака для класса, тем меньше коэффициент полезности этого признака для класса. Рассмотрим работу алгоритма при обучении классификатора: 1. Имеются вектора событий. При необходимости увеличиваем размерность векторного пространства, применяя к ним различные функции порождения признаков (Рис.1). 2. Масштабируем значения по всем каналам в отрезок [0..63]. 3. Составляем гистограммы значений для всех каналов по значениям [0..63] (Рис.2). 4. Отсеиваем значения гистограммы по некоторому порогу, получая область характерных значений (Рис.3). 5. Получаем коэффициент полезности признака по формуле 1.2. На Рис.4., для признака №1, чья масштабированная область значений изображена на верхнем отрезке (характерная область значений выделена красным цветом), полезность равна
Рис.4. Области значений масштабированной ( [0..63]) гистограммы для двух признаков после отсеивания по порогу 6. Среди всех пар признаков отбираются те, полезность которых выше порогового значения, или просто n самых полезных пар (Рис.5). Отобранные пары сохраняются в базе данных как характерные для класса с указанием коэффициента полезности.
Рис.5. Рабочая матрица области значений для пары каналов. Заштрихованы пересечения значений гистограмм выше порогового в двумерном пространстве
Рис.6. Получившаяся в результате обучения классификатора бинарная матрица (белым цветом обозначено значение TRUE, черным – FALSE). Такие матрицы для всех (или для наиболее полезных) пар признаков сохраняются в базе признаков данного класса В результате обучения мы получаем статистическую базу, содержащую попарные бинарные матрицы характерных областей значений для всех признаков (либо для заданного количества наиболее полезных), а также коэффициенты полезности каждого признака. При работе с данными, требующими классификации, для них также будут составляться попарные бинарные матрицы, подобно составленным при обучении, которые будут сравниваться с хранимыми в базе. По количеству совпадений и будет определяться мера принадлежности данных целевому классу. Имея помимо матриц с характерными значениями признаков также и коэффициенты полезности признаков для класса, можно использовать при тестировании не все признаки, а лишь некоторое количество наиболее полезных. Такой подход позволяет значительно сократить количество обрабатываемой информации. Т.к. матрицы попарные, то количество этих M матриц для N признаков: Это означает, что количество вычислений зависит от количества сравниваемых признаков как Коэффициент полезности для признаков тестируемой выборки определяется аналогично ключевой выборке: Работа обученного классификатора происходит следующим образом: 1. Загрузка значения коэффициентов полезностей признаков для данного класса (из файла c расширением .txt). 2. Загрузка попарных бинарных матриц характерных значений признаков. При заданном параметре количества приоритетных признаков среди матриц из базы извлекаются не все, а лишь соответствующие тем признакам, имеющим наибольший коэффициент полезности. Количество этих матриц с увеличением значения вышеуказанного параметра увеличивается квадратично. 3. Загрузка тестируемых данных из файла, составление гистограмм характерных значений (масштабированных в отрезок [0..63]), всех, или, если указано, отобранных по наиболее приоритетным признакам (п.2). 4. Определение коэффициента полезности каналов тестируемых данных по формуле 1.2. 5. Составление бинарных матриц для каналов тестируемых данных (аналогично матрицам, составляемым при обучении модели). 6. Матрицы, загруженные в п.2, сравниваются побитово при помощи логической операции AND (конъюнкция), при значении a&b = TRUE счетчик увеличивается на величину R, пропорциональную коэффициентам полезности четырех каналов (два канала ключевой выборки и два тестируемой выборки). При работе с каналами под номерами n и m, т.е. произведение коэффициентов полезностей для базовых матриц и рассчитанных в п.4 коэффициентов полезности для матриц, составленных при классификации данных.
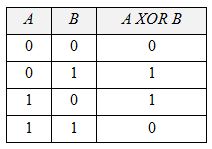
Преимущества решения Функциональные преимущества Известно, что принципиальным ограничением перцептронов является невыполнимость операции Рассмотрим выполнение рассматриваемым алгоритмом побитовых операций AND, OR, XOR. Таблица истинности для операции XOR выглядит следующим образом (Таблица 1): Таблица 1. Таблица истинности для операции XOR
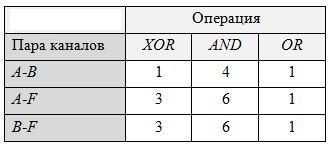
Применим порождающую функцию F сложения переменных, приведенных к численному виду. Таким образом, для обучения алгоритма выполнению операции достаточно матрицы 2х3 с использованием двух признаков (одна пара): A и F. Покажем, что двух исходных каналов и одного произведенного достаточно для безошибочного обучения операциям. После обучения операциям XOR, AND и OR из соответствующих битовых матриц получаем коэффициенты полезности, представленные в Таблице 2. Таким образом, задавая операнды и тип операции, будем рассматривать первое как распределение, а второе как искомый класс. Истинное значение матрицы будет совпадать с одним из истинных значений обученной матрицы при истинном результате логической операции, иначе – с одним из ложных. Таким образом, обучение алгоритма на таблице истинности логических операций позволяет верно классифицировать логические выражения в соответствие с правой частью таблицы истинности. Таблица 2. Коэффициенты полезности для различных битовых пар после обучения операциям XOR, AND и OR
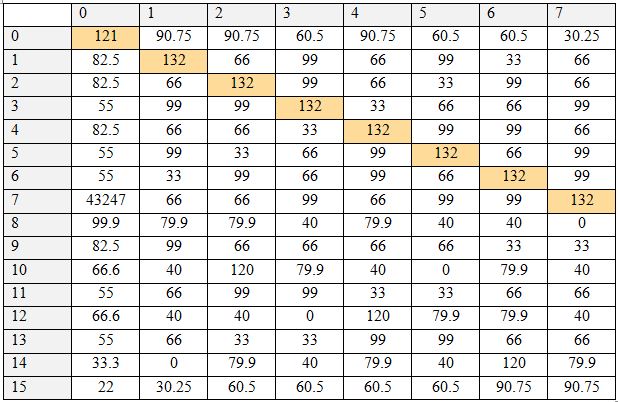
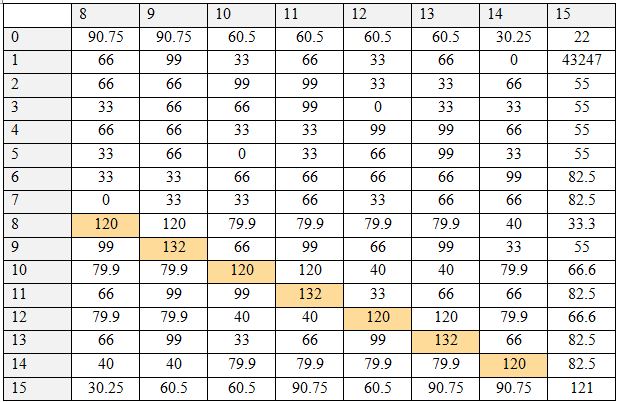
Было проведено исследование, определяющее исходную логическую функцию по ее таблице истинности для всех логических операций с двумя операндами. Результаты представлены в Таблице 3. По столбцам таблицы располагаются числа, характеризующие таблицу истинности. По строкам – предполагаемые функции (также обозначены числами). Таблица показывает величину соответствия – насколько данная таблица истинности соответствует данной гипотетической логической операции. В базе хранятся по три пары признаков для каждой операции в виде трех матриц и коэффициенты полезности признаков. Для тестируемой таблицы истинности также составляются три матрицы, рассчитываются коэффициенты полезности, после чего соответствующие матрицы сравниваются. При равенстве положительных элементов матриц величина совпадения увеличивается на вычисленное при помощи коэффициентов полезности число. Таблица 3. Таблица результатов, часть 1. По вертикали – номер таблицы истинности, по горизонтали – номер гипотетически проверяемой функции Таблица 4. Таблица результатов, часть 2. По вертикали – номер таблицы истинности, по горизонтали – номер гипотетически проверяемой функции Чем выше полезность, тем выше это число. Таким образом, происходит выполнение алгоритма сравнения признаков таблицы истинности с признаками очередной бинарной логической операции. Эти действия выполняются для всех хранящихся в базе логических операций, в результате чего для каждой из них имеется величина совпадения. Наибольшая величина совпадения означает ответ на вопрос, какой операции соответствует таблица истинности. Как видно, каждая таблица истинности получила единственное максимальное значение величины совпадения как раз для соответствующей ей функции, т.е. для каждой операции ответ был дан однозначно и верно. Цветом выделены значения, являющиеся максимальной величиной для данной таблицы истинности.
Тестирование и сравнение результатов Тестирование проводилось в два этапа: 1. Испытание правильности работы алгоритма на примере распознавания объектов на изображениях по цветовым характеристикам этого объекта. 2. Испытание скорости выполнения алгоритма на наборе данных и сравнение с существующими альтернативными методами. 3. Испытание точности работы алгоритма.
Для тестирования были выбраны два изображения, содержащие учебную доску (Рис.7). В качестве обучающей выборки были выбраны небольшие области 50х50 пикселей с доской на изображении. В качестве тестируемой выборки были выбраны все пиксели одного изображения. В качестве признаков были использованы яркости RGB пикселя, доли RGB пикселя, градация серого. Результатом работы алгоритма является окрашивание пикселя в серый цвет, яркость которого будет пропорциональна вероятности принадлежности ключевой выборке (Рис.8).
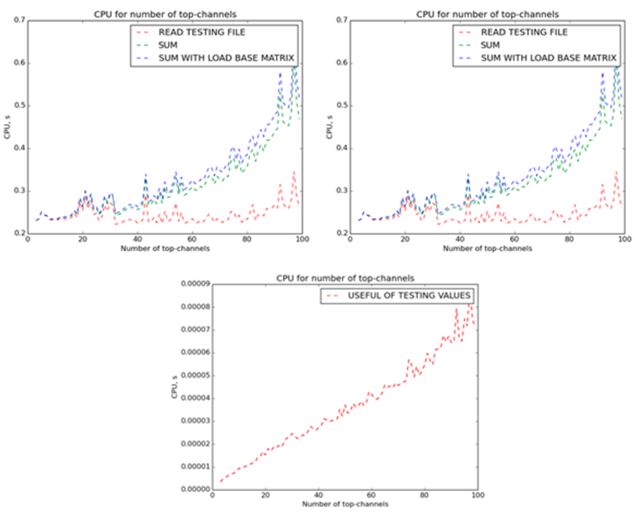
Для отображения зависимости количества затрачиваемого процессорного времени от количества исследуемых признаков, были проведены соответствующие тесты с использованием тестируемой выборки размерностью пространства признаков, равном 99, и количеством точек в 99-мерном пространстве, равном 5000. На Рис.9. приведены графики зависимости затрат процессорного времени на различные этапы выполнения алгоритма от количества исследуемых признаков. Количество исследуемых наиболее полезных признаков варьировалось в интервале от 3 до 99. Каждое значение времени было получено путем двадцатикратного повторения операции и взятия среднего арифметического. К сожалению, даже взятие среднего арифметического по двадцати повторениям не позволило избежать случайного разброса величин, однако все же можно определить наличие квадратичной зависимости от количества исследуемых полезных признаков для следующих этапов: загрузка базовых матриц, создание тестовых матриц, сравнение матриц, общее время выполнения алгоритма. Помимо этого, видна линейная зависимость времени для этапа расчета коэффициентов полезности для признаков тестируемой выборки. Видно, что на время считывания из файла количество используемых признаков не влияет, т.к. в данном случае все данные хранятся в одном файле. Но в случае хранения данных параллельно можно добиться линейного убывания затрат процессорного времени при уменьшении количества исследуемых признаков.
Рис.9. Графики зависимости затрат процессорного времени на выполнение различных стадий алгоритма в зависимости от количества приоритетных каналов
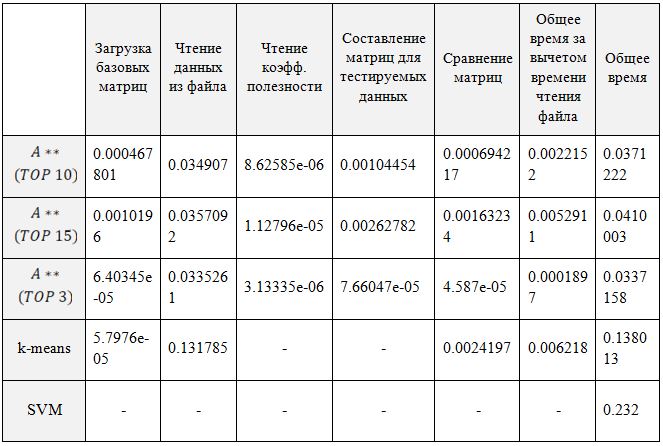
Рис.10. Данные класса А по 1-5 каналам, один из которых наиболее полезен С целью сравнения скорости работы алгоритма с двумя аналогами, методов опорных векторов и методом k-средних, была проведена серия экспериментов. Исследуемая выборка – файл, содержащий данные по пятнадцати признакам, из которых три являются наиболее важными. Количество пятнадцатимерных векторов в выборке – 10000, из которых первые 5000 относится к ключевому классу. В Таблице 5 приведены результаты измерения процессорного времени (в секундах), затраченного на выполнение этапов алгоритмов в сравнении с аналогами – методом опорных векторов и методом k-средних. Как видно из таблицы, за исключением времени считывания самого тестируемого файла, остальные показатели по скорости выигрывают у ближайшего конкурента по этому параметру – метода k-средних. Оставив десять признаков, получаем преимущество в скорости примерно в три раза, а для трех признаков время работы быстрее приблизительно в шестьдесят раз. Таблица 5. Затраты процессорного времени на выполнение алгоритмов. По горизонтали – алгоритмы. По вертикали – этапы выполнения алгоритма.
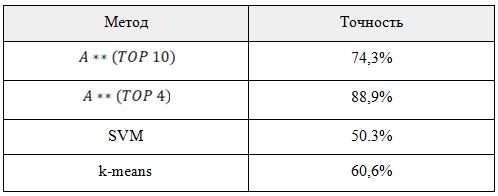
Тестирование точностиДля тестирования точности были сгенерированы наборы данных с высоким взаимным пересечением двух классов. Значения признаков класса А сгенерированы генератором случайных чисел в следующих промежутках: [-20, 20], [-15, 15], [-60, -35], [-80, 30], [50, 100], [-3, 70], [-80, 0], [-50, 0], [-40, -20], [55, 85] Значения признаков класса B сгенерированы генератором случайных чисел с равномерным распределением вероятности в следующих диапазонах: [-30, 30], [-10, 30], [-90, -40], [10, 50], [0, 70], [-3, 70], [-40, 0], [-25, 25], [-60, -40], [30, 70] Также была произведена замена пяти процентов данных случайными значениями в качестве имитации зашумления данных. Алгоритмы были обучены на сгенерированных наборах данных, после чего были проведены тесты, заключающиеся в том, чтобы разделить смешанные данные на два класса. Результаты тестирования показаны в Таблице 6. Как видно из таблицы, исследуемый алгоритм показал более высокие результаты по сравнению с SVM и k-means, причем при уменьшении количества исследуемых признаков точность работы увеличилась, так как признаки с меньшим коэффициентом полезности увеличивали количество совпадений, не являющихся ключевыми. Таблица 6. Сравнение точности алгоритмов
Выводы Целью данной работы являлись разработка и тестирование экспериментального алгоритма классификации данных с учителем. Исследования показали, что экспериментальный алгоритм способен классифицировать некоторые виды данных с более высокой скоростью, чем методы опорных векторов и k-средних, являющиеся также методами, обладающими высокой быстротой выполнения, и при этом обладает преимуществом в точности за счет отсутствия у предложенного алгоритма ряда недостатков, присущих вышеуказанным методам – чувствительность к выбросам, склонности к переобучению, проблеме медленной сходимости. Основным ограничением предложенного метода является отсутствие универсальности, т.е. возможность работы только с инерциальными типами данных. Таким образом, можно сделать вывод, что алгоритм способен не только стать более эффективным аналогом популярных алгоритмов классификации для решения определенного круга задач, но также может ускорить работу современных нейронных сетей в качестве альтернативы слоям нейронов как составная часть сложных систем классификации, что сделает их работу еще более доступной и дешевой. Библиографический список 1.C.C. Aggarwal. Data Classification: Algorithms and Applications. Chapman and Hall/CRC, 2014. References 1.C.C. Aggarwal. Data Classification: Algorithms and Applications. Chapman and Hall/CRC, 2014. |


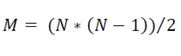 (1.3)
(1.3)