Оптимизация резонансных свойств фотонных кристаллов
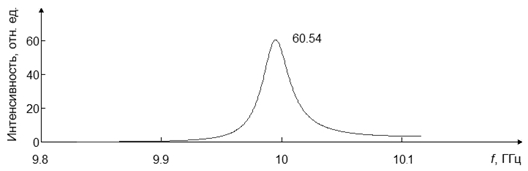
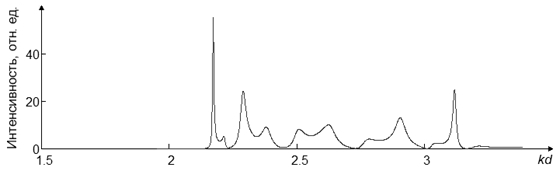
Optimization of the resonance properties of photonic crystalsУДК 535.63, 537.874 16.11.2016 Выходные сведения: Авторы: Authors: Ключевые слова: Keyword: Аннотация: Annotation: Одним из интересных и перспективных направлений современной радиофизики является разработка и изучение свойств фотонных кристаллов (ФК) и метаматериалов. Этими терминами в настоящее время обозначают разные объекты, обладающие, тем не менее, во многом сходными чертами. В первую очередь, это периодический характер их внутренней структуры, представляющей собой чередование диэлектрических или металлических элементов с различной геометрией и разными электрофизическими характеристиками и обуславливающей особенности взаимодействия с ними электромагнитных излучений. Говоря об этих особенностях, для ФК в первую очередь следует отметить наличие зонной структуры спектра собственных электромагнитных состояний таких объектов, выражающееся в формировании диапазонов частот, в которых излучение либо свободно проходит через кристалл (разрешенные зоны), либо интенсивно подавляется (запрещенные зоны) [1, 2]. Кроме того, большой интерес вызывает наличие у ФК ярко выраженной дисперсии, причем как частотной, так и пространственной, что открывает широкие возможности для их весьма разнообразных практических приложений [3-7]. Так, в работах [8-10] было показано, что при определенных соотношениях между длиной волны излучения и плотностью компоновки элементов в двумерном металлическом ФК возможна локализация излучения в центральной области структуры, которую можно трактовать как проявление кристаллом резонансных свойств. На рис. 1 показан типичный частотный спектр излучения, взаимодействовавшего с описанным выше кристаллом, элементы в котором образуют квадратную решетку 11 на 11 элементов, для случая, когда точка наблюдения находится в центральной области ФК. Расчет выполнен методом самосвязанных уравнений [11, 12]. Рис. 1. Частотная зависимость интенсивности поля в центральной области ЭК Из рисунка видно, что в пределах разрешенной зоны, расположенной в диапазоне значений kd (k – волновое число, d – период ФК) от 1,5 до 2,15, находятся несколько ярко выраженных максимумов, свидетельствующих о локализации поля в ФК, благодаря чему становится возможным создание резонаторных структур на основе ФК. Наибольшей амплитудой обладает первый максимум, возникающий на частоте перехода от запрещенной к разрешенной зоне, причем, как показали дополнительные исследования, это является типичным для любых двумерных регулярных ФК. Поскольку на данной частоте наблюдается максимальная локализация поля, именно при таких параметрах ФК проявляет ярко выраженные резонансные свойства. Как уже отмечалось, электромагнитное поле внутри такого резонатора оказывается локализованным по всей площади с максимумом в его центральной области. Его характеристики могут быть определены различными численными методами, общими для которых являются значительные затраты машинного времени, быстро растущие с увеличением протяженности структур. Целью настоящей работы являлось установление взаимосвязи между интенсивностью локализованного излучения в ФК различных размеров, что позволило бы избежать трудоемких расчетов при анализе резонансных свойств многоэлементных структур. В табл. 1 приведены значения интенсивности поля для структур, состоящих из разного количества элементов, при разных отношениях d/a, где a – радиус цилиндров. Здесь же представлены связывающие коэффициенты βn, показывающие во сколько раз увеличится интенсивность поля в резонаторе с увеличением количества элементов, составляющих его. Таблица 1
Коэффициенты связи
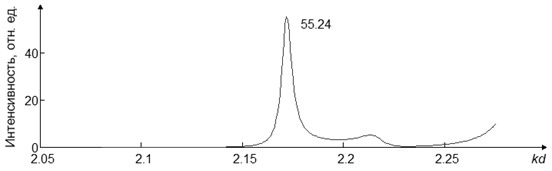
Как видно из таблицы, коэффициенты связи β9 – β15, полученные для структур при разных значениях d/a, приблизительно равны друг другу. Это дает возможность рассчитывать уровень интенсивности поля для резонаторов с разной геометрией. Проиллюстрируем вышесказанное, определив интенсивность поля в ФК, состоящем из 121 элемента с d/a = 13. Для этого необходимо знать интенсивность поля в простейшей структуре, образованной 81 элементом. Строгое численное моделирование показало, что эта величина равна 36,1. Используя соответствующий коэффициент из таблицы 1, получаем значение интенсивности в 55,1. Проверка данной оценки с помощью метода самосвязанных уравнений привела к результатам, представленным на рис. 2, хорошо согласующимися с вышеопределенной величиной. Следовательно, использование коэффициентов связи позволяет определять степень локализации излучения в протяженных ФК, опираясь лишь на расчеты, выполненные для малоэлементных структур.
Рис. 2. Относительная интенсивность поля для структуры, состоящей из 121 цилиндра, первый максимум Более того, поскольку полученный ряд коэффициентов хорошо укладывается в аппроксимирующую зависимость появляется возможность, оперируя лишь значением интенсивности в резонансной структуре, определить число элементов в ФК, позволяющем достичь требуемого уровня локализации излучения. Кроме того, в ходе численного моделирования было установлено, что безразмерная величина, равная произведению волнового числа, соответствующего резонансной частоте, на период ФК – kрезd, остается постоянной для любой частоты, если при этом не изменяется отношение d/a (табл. 2). Таблица 2 Произведение волнового числа в момент резонанса на период ЭК
Аппроксимацией значений из данной таблицы была получена следующая зависимость: Зная kрезd для разных отношений d/a, можно легко рассчитать наиболее эффективные значения радиуса цилиндров и расстояния между ними для создания резонаторов, работающих на заданной частоте. Например, определим оптимальную геометрию резонатора, работающего на частоте 10 ГГц (k = 209,44 м-1). Для этого необходимо с помощью формулы 2 определить значение kрезd для заданного отношения d/a, имея ввиду, что при уменьшении этой величины увеличивается интенсивность поля в структуре. Положим, что d/a = 10, этому соотношению соответствует значение kрезd = 2,395. Тогда, период ФК будет равен d = 11,435 мм, а радиус цилиндров в 10 раз меньше a = 1,1435 мм. По данным таблицы 1 (полученным для другого значения резонансной частоты) относительная интенсивность поля, например, для структуры из 81 элемента должна составить 60,59. Проверим этот результат, применяя строгий метод расчета к структуре с вышеопределенными параметрами (рис. 3). Рис. 3. Интенсивность поля в структуре, состоящей из 9 на 9 металлических цилиндров, на частоте 10 ГГц Видно, что изменение частоты практически не повлекли изменения уровня излучения в момент резонанса. Далее полученную интенсивность поля можно довести до желаемого значения, подобрав оптимальную форму структуры. Таким образом, в работе определены ряды коэффициентов, описывающих взаимосвязь интенсивности поля в резонаторах на основе ФК с разным количеством элементов и разной плотностью их компоновки. Это позволяет восстанавливать значения интенсивности локализованного излучения в многоэлементном ФК, зная лишь опорную величину интенсивности для простейшей структуры, и оптимизировать геометрию ФК для проявления им максимально выраженных резонансных свойств. Использование представленных в работе коэффициентов дает возможность существенного снижения затрат машинного времени на выполнение моделирования. В заключение отметим, что найденный ряд коэффициентов (таб. 1) с увеличением протяженности структур стремится к единице, что говорит о существовании предельных размеров резонаторов, при превышении которых уровень интенсивности локализованного в ФК излучения будет оставаться практически неизменным. Библиографический список 1. Joannopoulos J.D. Photonic Crystals: Molding the Flow of Light. Princeton Univ. Press. 2008. 304 p. References 1. Joannopoulos J.D. Photonic Crystals: Molding the Flow of Light. Princeton Univ. Press. 2008. 304 p. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

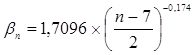 , (1)
, (1)