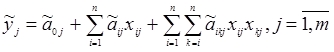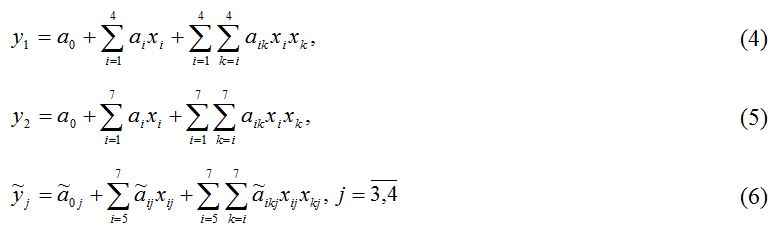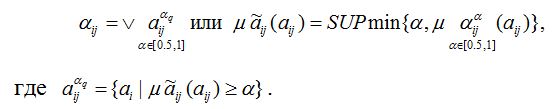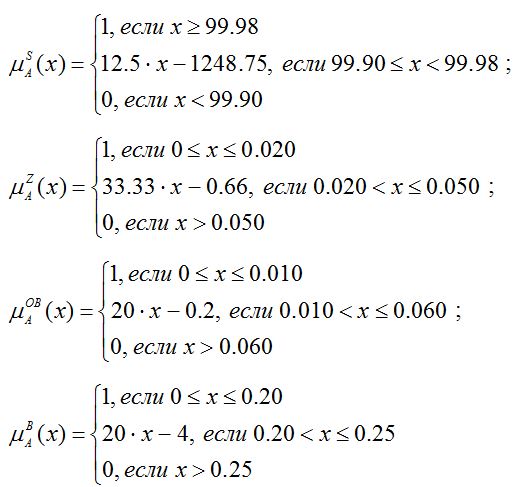Математические модели ХТС производства серы в нечеткой среде для информационных систем и технологий

Mathematical models of ChTS of sulfur production in fuzzy environment for information systems and technologies

УДК 502.65:622.276

23.08.2017
 

Выходные сведения:
Оразбаев Б.Б. Математические модели ХТС производства серы в нечеткой среде для информационных систем и технологий // ИТпортал, 2017. №3 (15). URL: http://itportal.ru/science/tech/metodika-postroeniya-matematicheski/

Авторы:
Оразбаев Б.Б., д.т.н., профессор кафедры Системного анализа и управления Евразийского национального университета им. Л.Н. Гумилева, Астана, Республика Казах-стан (010008, Казахстан, г.Астана, ул. Пушкина, 11),
e-mail: batyr_o@mail.ru

Authors:
Orazbayev B.B., Doctor of Technical Sciences, professor of the Department of System Analysis and Control of the Eurasian National University Gumilev, Astana, Republic of Kazakh-stan (010008, Kazakhstan, Astana, Pushkin street, 11.),
E-mail: batyr_o@mail.ru

Ключевые слова:
математическая модель, химико-технологическая система (ХТС), сера, нечеткая информация, информационные технологии, лицо, принимающее решение (ЛПР), нечеткие модели

Keyword:
mathematical model, chemical-technological system (ChTS), sulfur, fuzzy information, information technology, decision-maker, fuzzy models

Аннотация: 
На основе методов теории нечетких множеств и экспертных оценок разрабатывается методика построения моделей химико-технологических систем (ХТС) в условиях дефицита и нечеткости исходной информации. Предлагаемая методика описана на примере химико-технологической системы производства серы, которая характеризуются, как и другие слож-ные системы, многокритериальностью экономико-экологического характера и функционирует в условиях неопределенностью вызванной нечеткостью исходной информации. Разрабатываемые модели на основе предлагаемой методики могут быть в виде нечетких моделей, имеющие структуру нечетких уравнений множественной регрессии с нечеткими коэффициентами, и в виде лингвистических моделей, основанные на применение логических правил условного вывода. Модели первого типа (нечеткие модели) строятся в условиях измеримых (четких) входных параметров объекта (элемента ХТС) и нечетких значениях его выходных параметров, а модели второго типа, т.е. лингвистические модели, строятся при нечетких значениях (лингвистических) входных и выходных параметров объекта моделирования. В качестве преимущества предлагаемой методики построения нечетких и лингвистических моделей можно отметить что, она позволяет построить более эффективные модели объекта в условиях неопределенности, когда традиционные подходы не дают существенных результатов; в моделях, полученных на основе нечетких подходов, учитываются внутренние, содержательные связи основных параметров ХТС, которые не подлежат формализации, т.е. нечеткие модели позволяют учитывать всю гамму влияния внутренних и внешних параметров системы. Для достижения этих преимуществ необходимо иметь компетентных экспертов, правильно организовать и провести методов экспертной оценки, а также правильно применять методов теории нечетких множеств.

Annotation: 
Based on the methods of the theory of fuzzy sets and expert assessments, a methodology for constructing models of chemical-technological systems (ChTS) is developed in the conditions of indistinct initial information, which are used as part of information systems for optimizing the ChTS as efficient methods and means of information technology. The proposed technique is described in the example of the chemical-technological system of sulfur production, which, like other complex systems, is characterized by a multicriteria economic and ecological character and operates under conditions of uncertainty caused by the unclear initial information. The models developed on the basis of the proposed methodology can be in the form of fuzzy models having the structure of fuzzy equations of multiple regression with fuzzy coefficients, and in the form of linguistic models based on the application of logical rules of a conventional kind. Models of the first type (fuzzy models) are constructed under the conditions of measurable (clear) input parameters of the object (ChTS el-ement) and fuzzy values of its output parameters, and models of the second type, i.e. Linguistic models, are constructed with fuzzy values (linguistic) input and output parameters of the modeling object. As an advantage of the proposed methodology for constructing fuzzy and linguistic models, it can be noted that it allows us to build more efficient models of the object in conditions of uncertainty, when traditional approaches do not yield significant results; In models obtained on the basis of fuzzy approaches, internal, meaningful connections of the main ChTS parameters that are not subject to formalization are taken into account. Fuzzy models allow to take into account the whole gamut of influence of internal and external parameters of the system. To achieve these advantages, it is necessary to have competent experts, to properly organize and conduct expert assessment methods, and to apply correctly the methods of the theory of fuzzy sets.

Введение 

Технологические объекты, в которых протекают различные процессы нефтепереработки, в том числе процессы получения серы, и участвует человек в процессе управления ими, относятся к сложным химико-технологическим системам (ХТС).

Сложность этих ХТС и задач моделирования, оптимизации и управления ими проявляется в значительном числе и многообразии параметров, определяющих течение процессов, в большом числе внутренних связей между параметрами, в их взаимном влиянии, в неформализуемом действии человека, участвующего в контуре управления. Кроме того, при формализации и решении задач оптимизации режимов и управления ХТС возникает ряд проблем, связанных с множеством критериев, определяющих качество объекта. Многокритериальность исследуемых систем затрудняет разработку математического описания процессов и мероприятий, на основе которых осуществляется процедура оптимизации и управления [1, 2]. На практике часто из-за ненадежности, недостатков или отсутствия необходимых средств измерения, сбора и обработки статистических данных, собранная информация для описания исследуемой системы может оказаться в значительной степени неполной, достаточно неопределенной. Проведение специальных экспериментов для сбора недостающей информации, даже при возможности их проведения, часто оказывается экономически нецелесообразным. Основным источником информации в этих ситуациях является человек (специалист-эксперт, лицо, принимающее решение — ЛПР, технолог), который дает нечеткое описание проблемы, т.е. возникает проблема неопределенности, связанная с нечеткостью исходной информации [3, 4, 5, 6, 7].

Параметры, характеризующие производственные (экономические и экологические) показатели производства, описываются в виде математических моделей – системы уравнений, зависимостей и ограничений. Производственные объекты, ХТС, какими являются объекты глубокой нефтепереработки, разделены определенным образом на подсистемы и элементы, связанные ресурсами и различными потоками (материальные, информационные). При этом каждую подсистему можно описать однотипной системой уравнений обобщенного динамического баланса [8, 9]. Практическое применение такой модели производственных систем возможно при доступности всех составляющих и исходных данных, что часто затруднительно. Кроме того, данная модель довольно громоздкая, неудобная при реализации, т.е. неэффективная при решении задач оптимизации и управления в условиях многокритериальности, дефицита и нечеткости исходной информации. В этой связи в настоящее время актуальными являются методы разработки математических моделей с целью оптимизации и управления ХТС в нечеткой среде.  Целью данной работы является разработка методики построения  математических моделей многокритериальных ХТС условиях дефицита и нечеткости исходной информации на примере ХТС производства серы.

Результаты исследования и их обсуждение  

На основе методов теории нечетких множеств и экспертной оценки [3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16] предлагаем новый эффективный подход к разработке математических моделей технологических агрегатов ХТС, при наличии рассмотренных выше проблем многокритериальности и неопределенности, связанной с нечеткостью исходной информации. В качестве объекта исследования рассмотрим ХТС производства серы, в котором протекают процессы по производства серы из кислого газа. Целевая продукция  ХТС производства серы (гранулированная сера) направлена на решение экономико-экологических задач производства, в процессе работы должна отвечать определенным требованиям природоохранных мероприятий, т.е. характеризуются многокритериальностью экономико-экологического характера.

Как известно, при моделировании и оптимизации сложных ХТС в условиях неопределенности используется вероятностный подход, основанный на методах теории вероятностей и математической статистики [17, 18, 19]. Однако,  на практике не всегда при наличии неопределенностей выполняются аксиомы теории вероятностей (статистическая устойчивость объекта, возможность проведение экспериментов при одинаковых, неизмененных условиях и т.д.), что показывает неправомерность применения этих методов. Более того, в случаях, когда есть основания считать, что процессы или системы ведут себя по вероятностным законам, дефицит информации, невозможность или дороговизна получения достоверных статистических данных толкают на иные пути описания реальных процессов в производственных системах, на разработку нестатистических, например, нечетких методов моделирования объектов. Один из перспективных путей в этом направлении опирается на методы теории нечетких множеств [3, 6, 10]. Таким образом, проблему неопределенности из-за нечеткости исходной информации можно решить созданием математического аппарата для описания и исследования нечетко определенных объектов.

К достоинствам методов построения нечетких и лингвистических моделей можно отнести: они позволяют получить эффективные модели объекта в условиях неопределенности, когда традиционные подходы не дают существенных результатов; в моделях, полученных на основе нечетких подходов, учитываются внутренние, содержательные связи основных параметров системы, которые не подлежат формализации, т.е. нечеткие модели позволяют учитывать всю гамму влияния внутренних и внешних параметров процесса. Однако при построении нечетких моделей возникают свои специфические проблемы, например, связанные с проведением экспертного опроса, построением функции принадлежности нечетких параметров, определением структуры условного логического вывода, нечетких регрессионных уравнений и т.д.

При построении моделей ХТС, представляющей собой комплекс взаимосвязанных агрегатов различного типа (технологические установки) с различной исходной информацией, приходится использовать комбинированную информацию. В этом случае модели отдельных объектов, т.е. элементов ХТС могут быть построены разными методами, причем должна быть учтена возможность объединения этих моделей в пакет для моделирования работы системы в целом. На практике, при исследовании некоторого объекта, статистические данные для оценки одних параметров могут быть достаточны, а для других параметров – недостаточны или вообще отсутствовать. Параметры таких объектов оцениваются методами, основанными на использовании информации различного характера и объединяющими вышеописанные методы и традиционные подходы к анализу систем.

В результате анализа и обобщения возможных подходов моделирования сложных систем при нечеткости исходной информации в данной работе на примере ХТС производства серы предложена методика построения моделей химико-технологических систем в нечеткой среде, включающие следующие основные этапы:

1. Выбираются необходимые для построения модели входные  и выходные  параметры объекта, т.е. элемента ХТС, которые являются лингвистическими переменными ( нечеткие подмножества, X, Y – универсальные множества). Входные параметры могут быть четкими т.е. .

2. Проводится сбор информации и на основе экспертной процедуры определить терм-множество ( нечетких параметров, описывающих состояние элемента ХТС, т.е. исследуемого объекта.

3. Если xiÎXi, т.е. входные параметры объекта четкие (детерминированы), то определяется структура нечетких уравнений множественной регрессии  (решение задачи структурной идентификации).

4. Строятся функции принадлежности нечетких параметров объекта  и коэффициентов модели.

5. Если и входные и выходные параметры объекта нечеткие, то строятся лингвистические модели системы и формализуются нечеткие отображения , определяющие связи между лингвистическими переменными  и . Перейти к пункту 7.

6. Если выполняются условия пункта 3, то оценить нечеткие значения коэффициентов () выбранных функций  (решение задачи параметрической идентификации). Перейти к пункту 8.

7. Определяются нечеткие значения параметров объекта и выбираются  их числовые значения из нечеткого множества решений.

8. Проверяется условие адекватности модели. Если условие выполняется, то модель рекомендуется для исследования, оптимизации и управления объектом, ХТС, в противном случае определить причину неадекватности и вернуться к предыдущим пунктам для уточнения модели.

Дадим пояснения к основным пунктам приведенной методики.

В пункте 1 выбираются наиболее информативные переменные, которые характеризуют работы объекта. Для удобства диапазоны изменения нечетко описываемых параметров задаются в виде отрезков, с указанием минимального () и максимального () значения. Эти отрезки, в зависимости от суждений специалистов-экспертов, разбиваются на несколько интервалов дискретизации (кванты):

        .

Для построения терм-множества состояний (пункт 2) каждый квант выбранных параметров словесно характеризуется соответствующими нечеткими терминами. Например, если  – качество вырабатываемой серы, то его можно описать через термы:

 ={очень  низкое,  низкое,  среднее,  высокое, очень высокое}.

Принятое терм-множество является совокупностью значений лингвистических переменных, описывающих работу исследуемого объекта. Каждый квант, получаемый в i-ом пункте, характеризуется определенным термом. Этому терму соответствует нечеткое множество, которое описывается функцией принадлежности на соответствующем ей уровне градации.

Для определения структуры нечетких уравнений множественной регрессии (пункт 3) можно использовать подход нечеткого регрессионного анализа. На этом этапе определяющее значение имеет качественный анализ объекта, в результате которого выявляются основные параметры, влияющие на функционирование, их взаимосвязи и выбирается метод для идентификации структуры модели.

Построение функции принадлежности нечетких параметров (пункт 4) является одним из основных этапов при моделировании и оптимизации сложных объектов, ХТС с применением методов теории нечетких множеств. Основным способом восстановления аналитического вида этой функции является графическое построение кривой степени принадлежности того или иного параметра соответствующему нечеткому множеству. На основе полученного графика подбирается такой вид функции, который наилучшим образом аппроксимирует его. После этого идентифицируются параметры выбранной функции.

На основе опыта моделирования технологических агрегатов различных ХТС нефтепереработки в нечеткой среде нами предлагается следующая структура функции принадлежности:

                                                              (1)

где  – функция принадлежности параметров нечеткому множеству , характеризующая значения выходных параметров; p –номер кванта; –параметр, который находится при идентификации функции принадлежности и определяющий уровень нечеткости; – коэффициенты для изменения области определения термов и формы графика функции принадлежности нечетких параметров;   – нечеткая   переменная, наиболее соответствующая данному терму (в кванте p), для которой .

Лингвистическая (качественная) модель объекта (пункт 5) строится по результатам обработки экспертной информации с использованием логических правил условного вывода: IF  THEN .  Для удобства ее можно оформить в виде таблицы, где словесно (нечетко) указаны различные значения входных лингвистических переменных  и соответствующие этим вариантам значения выходных лингвистических переменных — . Таблица должна заполняться с использованием выбранного терм-множества в пункте 2.

На основе модели, полученной таким образом, формализуются нечеткие отображения , определяющие связь между входными и выходными параметрами. Нечеткие отображения для кванта р можно определить следующим образом: . Для удобства применения нечеткого отображения  в расчетах нужно построить матрицы нечетких отношений — , например, в общем случае для выделенных квантов:

Для определения оценки параметров выбранной функции в пункте 3 (параметрическая идентификация) можно воспользоваться критерием минимизации отклонения нечетких значений выходного параметра , полученных по модели, от его выборочных нечетких значений, полученных на основе экспертной оценки .

На этом этапе основным вопросом является выбор способа оценивания неизвестных параметров, обеспечивающего необходимые свойства исследуемого объекта, т.е. элемента ХТС. При этом нечеткие модели имеют вид нечеткого уравнения множественной регрессии [3, 6]:

Пункт 7 данной методики построения нечетких моделей заключается в применении композиционного правила вывода: Bj = Ai ° Rij.

С помощью этого правила можно осуществлять расчет выходных переменных, например, на основе максиминного произведения:

                                                 (2)

Пусть  – измеренные (оцененные экспертами) значения входных переменных, тогда искомое множество, которому принадлежат текущие измеряемые значения входных переменных, определяется как множество, для которого измеряемые значения имеют наивысшую (максимальную) степень принадлежности:

Прогнозируемые значения выходных переменных (нечеткие значения) определяются в виде соответствующих функций принадлежностей (2).

Конкретные числовые значения выходных параметров  из нечеткого множества решений определяются из следующего соотношения:

                                                                                    (3)

т.е. выбираются те значения входных параметров, для которых достигается максимум функции принадлежности.

Задачей заключительного этапа методики (пункт 8) является проверка соответствия модели объекту. Модель считается адекватной моделируемому объекту, если найденные с ее помощью на компьютере характеристики объекта совпадают с заданной степенью точности, реальными данными, полученными экспериментально на самом объекте.

Как правило, в качестве критерия адекватности, являющегося мерой соответствия модели объекту, используется величина рассогласования расчетных (модельных)  и реальных (экспериментальных) – данных: . Кроме того, выбирается величина допустимого уровня рассогласования – . Модель считается адекватной, если  

В случае неадекватности математическая модель определяются источники неадекватности. Причиной, источниками неадекватности модели  может быть недооценка значимости какой-нибудь существенной переменной и недоучет ее в модели, неправильная или неполная структура нечетких уравнений, ошибка при параметрической идентификации и т.д. После этого осуществляется возврат к соответствующему пункту алгоритма для доработки модели.

Практическое применение разработанной методики построения математических моделей ХТС в нечеткой среде

На основе предложенной выше методики разрабатываем модели реакторов блока производства серы ХТС производства серы функционирующих Атырауского НПЗ. В основу математической модели термореакта F-001 и реактора Клауса R-001 положены статистические данные, экспертная информация обработанные методами теории нечетких множеств, а также уравнения материального и теплового балансов.

В результате обработки экспериментально-статистических и экспертных данных, а также применяя идею метода последовательного включения регрессоров, на основе информации различного характера получена следующая структура системы уравнений множественной нечеткой регрессии и условного логического вывода, являющихся моделями исследуемых реакторов:

где y1,  y2  – соответственно, выход серы с термореактора и реактора Клауса;  качественные показатели получаемой серы, соответственно, массовая доля серы (в зависимости от сорта не менее от 99.20 до 99.98 %), массовая доля воды продукции (в зависимости от сорта не более от 1.0 до 0.2%); x1 – загрузка, расход сырья на входе в термореактор  F-001 (26–28 т/ч); x2 – температура термореактора F-001 (1000–1413о С); x3 — температура выхода термореактора (180–350оС); x4– расход воздуха горения на термореакторе F-001 (200–700 нм/м3);  x5 – загрузка сырья в реактор Клауса R-001(6–8 т/ч); x6 – температура на входе реактора R-001 (180–290оС); x7 – температура на выходе реактора R-001 (300–345оС);  – идентифицируемые коэффициенты регрессии (четкие и нечеткие со знаком ~), соответственно: свободный член; учитывающие линейные влияния (xij),  квадратные и взаимные влияния (xij, xkj), на выходные параметры реактора.

Как видно, модели описывающие выход продукции с реакторов имеют вид множественной регрессии, соответственно идентифицированы экспериментально-статистическими методами, а модели оценивающие качества серы имеют вид нечетких уравнений множественной регрессии и получены на основе качественной информации от специалистов-экспертов.

Идентификация коэффициентов регрессии в моделях (4)‒(6) осуществлены известными методами параметрической идентификации, на основе методов наименьших квадратов с применением пакета программ REGRESS (Кузнецов А.Г., Оразбаев Б.Б.).

Результаты параметрической идентификации моделей, определяющих зависимость выхода серы с реакторов, имеют вид (7)‒(8):

Для идентификации неизвестных нечетких коэффициентов  и  в уравнениях (6) нечеткие множества, описывающие качественные показатели продукции, разбиты на следующие множества уровня α = 0,5; 0,75; 1. В соответствии с выбранным уровнем наблюдается значения входных  хij и выходных параметров на каждом уровне ,

Для каждого уровня  моделей качественных показателей серы (6), можно представить в виде системы уравнения множественной регрессии, тогда задача идентификации их коэффициентов  сводится к классическим задачам оценивания параметров множественной регрессии. Для решения последней задачи можно использовать известные алгоритмы или стандартные программы множественной регрессии. Нами применен вышеуказанный пакет программ REGRESS.

Полученные значения коэффициентов  модели (6) объединены с использованием следующего соотношения

Таким образом, математические модели, описывающие нечеткую зависимость качественных показателей серы, например, массовая доля серы 3 от входных параметров хi, i= (x1 – температура термореактора F-001(1000–1413 оС); x2– расход воздуха горения на термореакторе F-001 (200–700 нм/м3);  x3 – температура реактора R-001 (280–300оС)) имеют вид;

Исследование и построение лингвистических моделей определения качества получаемой серы. Для оценки качества получаемой серы на основе логического правила условного вывода и базы знаний построены лингвистические модели, описывающие зависимость качества серы (сортность) от массовой доли серы, массовой доли золы, массовой доли органических веществ и массовой доли воды. Эти модели реализуют лингвистическую зависимость, представляющей собой продукционную базу знаний:

-If МS99,98%МZ0,02%МОВ0,01%МВ0,2%, Then QS — «высокое», Else

-If МS99,95%МZ0,03%МОВ0,03%МВ0,2%, Then QS — «выше среднего»,

Else

-If МS99,90%МZ0,05%МОВ0,06%МВ0,2%, Then QS — «среднее», Else

-If МS99,50%МZ0,20%МОВ0,25%МВ0,2%, Then QS — «ниже среднего», Else

-If МS99,20%МZ0,40%МОВ0,50%МВ1,0%, Then QS — «низкое».

В вышеприведенной лингвистической модели оценки качества серы приняты следующие обозначения МS — массовая доля серы; МZ – массовая доля золы; МОВ – массовая доля органических веществ; МВ – массовая доля воды;  — нечеткое ограничение  «не более»; QS – качество серы.

На производстве «высокое качество» серы относится к сорту 9998; «выше среднего» – 9995; «среднее» – 9990; «ниже среднее» – 9950; «низкое» – 9920.

Как видно из лингвистической модели качество серы, главным образом, зависит от состава серы. Поэтому на практике при нарушении остальных требований (массовая доля золы, органических веществ и воды) качество серы определяется в зависимости от значения первого критерия (требования). На основе этого база знаний дополнена другими условиями и выводами, например:

-If МS99,98%МZ0,03%МОВ0,03%МВ0,2%, Then QS — «выше среднего»,

-If МS99,95%МZ0,04%МОВ0,05%МВ0,5%, Then QS — «среднее»,

-If МS99,90%МZ0,25%МОВ0,30%МВ0,3%, Then QS — «ниже среднего»,

-If МS99,50%МZ0,35%МОВ0,50%МВ0,5%, Then QS — «низкое».

Таким образом, при нарушении требований к массовой доли золы, органических веществ и воды, сортность качества серы, как правило, определяется  одним сортом ниже.

Приведенные лингвистические модели в виде продукционной базы знаний позволили формализовать и описать качества и сортность получаемой серы. Функции принадлежности нечетких параметров и показателей качества серы, могут быть построены на основе разработанного в [15] алгоритма построения функции принадлежности, т.е. на основе экспертной информации. Например, функции принадлежности нечетких показателей, описывающие «высокое качество» серы имеет следующие виды [3, 14]:

где  – соответственно, функции принадлежности, описывающие нечеткие показатели состава серы, золы, органических веществ и воды.

         Заключение

В работе предложена методика разработки моделей ХТС на примере установки производства серы в условиях дефицита и нечеткости исходной информации, основанная на применение методов теории систем, методов экспертных оценок и теории нечетких множеств. Дано описание основных пунктов реализации предложенной методики. На основе предлагаемой методики могут быть разработаны: нечеткие модели, имеющие структуру нечетких уравнений множественной регрессии с нечеткими коэффициентами, и лингвистические модели, основанные на применение логических правил условного вывода. Выделены преимущества предлагаемой методики и возможные проблемы при ее реализации. Приведен пример практического применения разработанной методики при построении моделей ХТС производства серы Атырауского НПЗ.

Библиографический список

1.Мушик Э., Мюллер П. Методы принятия технических решений. -М.: Мир, 1990. -208с.
2.Канеман Д., Словик П., Тверский А. Принятие решений в неопределенности: Правила и предубеждения.- Харьков: Гумм. Центр, 2005. – 632 с.
3.B.B. Orazbaev, Orazbayeva K.N., Utenova B.E. Development of Mathematical Models and Modeling of Chemical Engineering Systems under Uncertainty// Theor. Foundations of Chem. Eng. // 2014. Vol. 48, No 2, -P. 138-147.
4.Оразбаев Б.Б., Оспанов Е.А., Оразбаева К.Н., Курмангазиева Л.Т. Гибридный метод разработки математических моделей химико-технологической системы в условиях неопределенности // Математическое моделирование. 2017. Т. 29. № 4. -С. 30-44.
5.Рыков А.С., Оразбаев Б.Б. Системный анализ и исследование операции: Экспертные оценки. Методы и применение. -М.: МИСиС, 1995. -115с.
6.Оразбаев Б.Б. Теория и практика методов нечетких множеств. Министерство науки и образования РК, -Бастау, -Алматы, 2014, 488 с.
7.Dubois D. The role of fuzzy sets indecision sciences: Old techniques and new directions // Fuzzy Sets and Systems. V. l. No 184. – 2011. –C. 3–28.
8.Викулов В.Г., Гурман В.И., Данилина Е.В и др. Эколого-экономическая стратегия развития региона: Математическое моделирование и системный анализ. -Новосибирск: Наука, 1990. -184 с.
9.Orazbaeva K.N., Serikov F.T., Orazbaev B.B. Effective algorithm of devel-oping the model of economic-ecological systems of oil and gas manufacture under the illegibility of the initial information //International journal of scientific articles «Science and technology», book 4. –Р.18-22.
10. Рыжов А.П. Элементы теории нечетких множеств и ее приложений. –М.: МГУ. 2003. -81 с.
11. Оразбаев Б.Б. Экспертные системы для медицинской диагностики с применением методов теории нечетких множеств // Журнал ИТпортал, 2016. №4 (12). –С. 1-16, URL: http://itportal.ru/science/tech/ekspertnye-sistemy-dlya-meditsinsko/
12. Джарратано Д., Райли Г. Экспертные системы: принципы разработки и программирование: Пер. с англ. –М. : Изд. дом «Вильямс», –2006. –1152 с.
13. Моисеева Т.Ф. Методы и средства экспертных исследований: учебник – М.: МПСИ, –2004. –347 с.
14. Оразбаев Б.Б., Кульжанов Д. У., Оразбаева К. Н. Исследование и описание процесса производства бензола на основе методов экспертных оценок // Новости науки Казахстана, №2(124). 2015. –С. 172-186.
15. Оразбаева К.Н. Применение методов экспертных оценок при разработке математического обеспечения АСУ комплексом производства бензола// Научно-технический журнал «Автоматизация, телемеханизация и связь в нефтяной промышленности», ВАК РФ, –Москва: ВНИИОЭНГ, №9, 2009. –С.41-45.
16. Мешалкин В.П. Экспертные системы в химической технологии. -М.: Химия, 1995. -350 с.
17. Гмурман, В.Е. Теория вероятностей и математическая статистика: Учеб. пособие -12-е изд., перераб. -М.: Высшее образование, 2006. -479 с.
18. Балдин К.В. Теория вероятностей и математическая статистика: учебник. – М.: Дашков и К, 2010 г;
19. Zhi-Wen Zhao, De-Hui. Wang Statistical inference for generalized random coefficient autoregressive model. Mathematical and Computer Modelling. Vol. 56, 152-166. 2012.
20. B.B. Orazbaev, B.E. Utenova, S. Iskakova Information systems for optimisation and control of sulphur production units // 4-th Int. academic research conference on business, education, nature and technology. USA. Seattle. 2013. PP. 430-433.

References

1.Mushik E., Myuller P. Metody prinyatiya tekhnicheskikh resheniy. -M.: Mir, 1990. -208s.
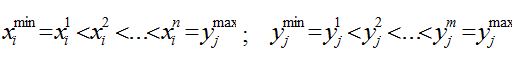2.Kaneman D., Slovik P., Tverskiy A. Prinyatiye resheniy v neopredelennosti: Pravila i predubezhdeniya.- Khar’kov: Gumm. Tsentr, 2005. – 632 s.
3.B.B. Orazbaev, Orazbayeva K.N., Utenova B.E. Development of Mathematical Models and Modeling of Chemical Engineering Systems under Uncertainty// Theor. Foundations of Chem. Eng. // 2014. Vol. 48, No 2, -P. 138-147.
4.B.B., Ospanov Ye.A., Orazbayeva K.N., Kurmangaziyeva L.T. Gibridnyy metod razrabotki matematicheskikh modeley khimiko-tekhnologicheskoy sistemy v usloviyakh neopredelennosti // Matematicheskoye modelirovaniye. 2017. T. 29. № 4. -S. 30-44.
5.Rykov A.S., Orazbayev B.B. Sistemnyy analiz i issledovaniye operatsii: Ekspertnyye otsenki. Metody i primeneniye. -M.: MISiS, 1995. -115s.
6.Orazbayev B.B. Teoriya i praktika metodov nechetkikh mnozhestv. Ministerstvo nauki i obrazovaniya RK, -Bastau, -Almaty, 2014, 488 s.
7.Dubois D. The role of fuzzy sets indecision sciences: Old techniques and new directions // Fuzzy Sets and Systems. V. l. No 184. – 2011. –S. 3–28.
8.Vikulov V.G., Gurman V.I., Danilina Ye.V i dr. Ekologo-ekonomicheskaya strategiya razvitiya regiona: Matematicheskoye modelirovaniye i sistemnyy analiz. -Novosibirsk: Nauka, 1990. -184 s.
9.Orazbaeva K.N., Serikov F.T., Orazbaev B.B. Effective algorithm of developing the model of economic-ecological systems of oil and gas manufacture under the illegibility of the initial information //International journal of scientific articles «Science and technology», book 4. –P.18-22.
10.Ryzhov A.P. Elementy teorii nechetkikh mnozhestv i yeye prilozheniy. –M.: MGU. 2003. -81 s.
11.Orazbayev B.B. Ekspertnyye sistemy dlya meditsinskoy diagnostiki s primeneniyem metodov teorii nechetkikh mnozhestv // Zhurnal ITportal, 2016. №4 (12). –S. 1-16, URL: http://itportal.ru/science/tech/ekspertnye-sistemy-dlya-meditsinsko/
12.Dzharratano D., Rayli G. Ekspertnyye sistemy: printsipy razrabotki i programmirovaniye: Per. s angl. –M. : Izd. dom «Vil’yams», –2006. –1152 s.
13.Moiseyeva T.F. Metody i sredstva ekspertnykh issledovaniy: uchebnik – M.: MPSI, –2004. –347 s.
14.Orazbayev B.B., Kul’zhanov D. U., Orazbayeva K. N. Issledovaniye i opisaniye protsessa proizvodstva benzola na osnove metodov ekspertnykh otsenok // Novosti nauki Kazakhstana, №2(124). 2015. –S. 172-186.
15.Orazbayeva K.N. Primeneniye metodov ekspertnykh otsenok pri razrabotke matematicheskogo obespecheniya ASU kompleksom proizvodstva benzola// Nauchno-tekhnicheskiy zhurnal «Avtomatizatsiya, telemekhanizatsiya i svyaz’ v neftyanoy promyshlennosti», VAK RF, –Moskva: VNIIOENG, №9, 2009. –S.41-45.
16. Meshalkin V.P. Ekspertnyye sistemy v khimicheskoy tekhnologii. -M.: Khimiya, 1995. -350 s.
17. Gmurman, V.Ye. Teoriya veroyatnostey i matematicheskaya statistika: Ucheb. posobiye -12-ye izd., pererab. -M.: Vyssheye obrazovaniye, 2006. -479 s.
18. Baldin K.V. Teoriya veroyatnostey i matematicheskaya statistika: uchebnik. – M.: Dashkov i K, 2010 g;
19. Zhi-Wen Zhao, De-Hui. Wang Statistical inference for generalized random coefficient autoregressive model. Mathematical and Computer Modelling. Vol. 56, 152-166. 2012.
20. B.B. Orazbaev, B.E. Utenova, S. Iskakova Information systems for optimisation and control of sulphur production units // 4-th Int. academic research conference on business, education, nature and technology. USA. Seattle. 2013. PP. 430-433.