Автоматизированные инструментальные средства оптимизации исходных кодов больших программных систем
Automated tools for optimizing the source code of large softwareУДК 004.021 06.10.2017 Выходные сведения: Авторы: Authors: Ключевые слова: Keyword: Аннотация: Работа выполнена при финансовой поддержке РФФИ (Российский Фонд Фундаментальных Исследований) и Министерства образования и науки Республики Северная Осетия – Алания в рамках научного проекта № 17-41-15081217. Annotation: This work carried out with the financial support of RFBR (Russian Foundation for basic Research) and the Ministry of education and science of the Republic of North Ossetia – Alania in the framework of scientific project No. 17-41-15081217. 1. Введение Целью исследований, выполненных в рамках гранта РФФИ № 17-41-15081217, является создание технологии, обеспечивающей автоматизацию процессов оптимизации [1, 2, 3] пользовательских исходных программных кодов на основе объективно сформулированных критериев качества. Основным научным результатом работы стала система дискретных моделей, представляющих собой формальную постановку поиска оптимальной декомпозиции [3, 4, 5] пользовательской программной системы, минимизирующей время работы с внешней [6, 7] медленной памятью (глава 2 — задачи (7), (8)). Для решения этих задач предложены эффективные алгоритмы (глава 3), не использующие комбинаторных процедур. Прикладным результатом стала программная реализация методов решения оптимизационных моделей: В частности, был создан автоматизированное инструментальное средство, дополняющее возможности популярной среды разработки MS Visual Studio модулем оптимальной декомпозиции. Выполнены тестирование и отладка программного продукта. Идея метода оптимальной декомпозиции программной системы заключается в минимизации времени работы с медленной памятью (жестким диском, флэш- или SSD-памятью и т.д.). Метод актуален в том случае, когда система функционирует в условиях недостатка быстрой памяти, а точнее, когда размер исполняемого кода намного превышает доступный объем оперативной памяти ЭВМ и фрагментация системы на подпрограммы неизбежна. Актуальность метода провоцируется с одной стороны широким распространением инструментальных средств быстрой разработки, а с другой с растущими требованиями к функциональности информационно-управляющих и информационно-поисковых систем различного назначения. Предлагаемый в работе подход к оптимальному разбиению (декомпозиции) исходного кода опирается на анализ пользовательского алгоритма, структура которого, для удобства формулировок, описана в терминах теории графов [8, 9, 10, 11]. Дерево переходов состояний описывает последовательность вызова элементарных неделимых программных единиц. В прикладной программной разработке, реализованной в рамках данной работы, в качестве элементарной единицы была принята функция, так как в состав большинства операционных систем включены удобные средства оформления пользовательского объектного кода в виде библиотек функций. К примеру, в ОС Windows набор функций подсистемы можно оформить в виде динамически подключаемой библиотеки (dynamic link library — DLL). Минимизация времени на обслуживание операций загрузки подобных библиотек составляет смысл оптимизации работы с медленной памятью.
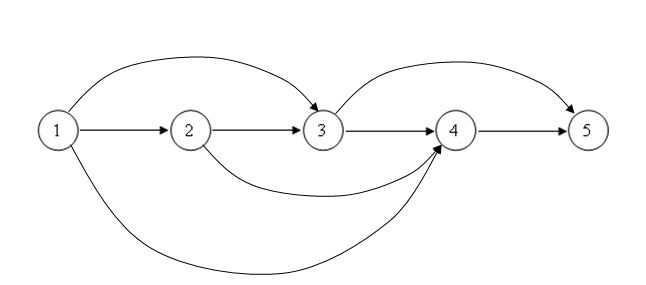
2. Материалы и методы Для программ простейшей линейной структуры [12, 13, 14] задачу выбора оптимального состава подсистем, минимизирующего время работы программы с медленной памятью можно сформулировать в терминах теории графов в виде задачи поиска кратчайшего пути. Данный подход нагляднее представить на следующем примере: Пусть пользовательский алгоритм содержит 4 функции, размер каждой из которых равен (в условных единицах): 1, 1, 2, 2. Путь верхняя граница оперативной памяти, доступной программе 4 единицы, тогда все возможные варианты подсистем удобно представить в виде графа (рис.1), на котором каждая вершина — это состояние программы (текущее состояние вектора данных), а дуги — это подсистемы, переводящие программу из одного состояния в другое. К примеру, дуга (1,2) соответствует подсистеме, включающей только первую функцию, а дуга (3,4,5) — это подсистема, содержащая функции 3 и 4. Граф на Рис.1 содержит только варианты подсистем, суммарный размер функций которых меньше либо равен 4. Рис.1. Граф вариантов подсистем. В том случае, если накладные расходы времени на загрузку модуля с внешнего носителя в ОП одинаковы для каждой подсистемы (т.е. длина всех дуг равна некоторой константе, зависящей только от аппаратных характеристик пользовательской ЭВМ), задача имеет 2 эквивалентных решения, соответствующих двум возможным кратчайшим путям: 1) (1 — 3 — 5) Первый модуль включает функции «1» и «2», а второй — функции «3» и «4». 2) (1 — 4 — 5) Первый модуль включает функции «1», «2» и «3», а второй — только функцию «4». Значение верхней границы ОП (в рассмотренном выше примере, взятое равным 4) определяется разработчиком прикладного ПО на основе характеристик целевых аппаратных систем — указывается в виде «минимальных» требований к ЭВМ в соответствующем разделе технической документации. Простые линейные системы (в которых последовательность вызова функций никогда не меняется, независимо от входных данных) больших масштабов на практике встречаются крайне редко. Наличие условных операторов в коде системы обуславливает возможность существования множества способов завершения программы. В этом случае термин «производительность» может требовать уточнения, так как время работы программы зависит от последовательности вызова функций. В данной работе предлагается подход, основанный на «пессимистической» оценке вероятностей операторных переходов, основанный на том, что для оценки качества пользовательского кода выбирается наиболее протяженный по длине путь, составленный из последовательных вызовов функций. Аналогично, для зацикленных программ (систем мониторинга окружающей среды, распознавания, АСУТП непрерывных производственных процессов и подобных систем) выбирается участок, представляющий собой контур максимальной длины. Важно отметить, что в большинстве систем в структуре алгоритма [15] присутствуют как контура[16, 17, 18, 19], так и варианты завершения. В таком случае, участок зацикливания имеет безусловный приоритет по сравнению с линейным участком (в условиях, когда вероятности переходов в условных операторах заранее не известны), так как время зацикливания в одном из контуров теоретически может стремиться к бесконечности. С учетом данных положений, процесс выбора оптимального состава подсистем, минимизирующего работу с медленной памятью, можно разбить на два этапа: На первом решается задача минимизации времени работы с внешней (медленной памятью) в максимальном контуре:
где Неизвестными в задаче (8) являются переменные На втором этапе выполняется поиск оптимального состава подсистем для конечного участка, соответствующего максимальному пути из начального состояния программы в один из вариантов завершения (3). где
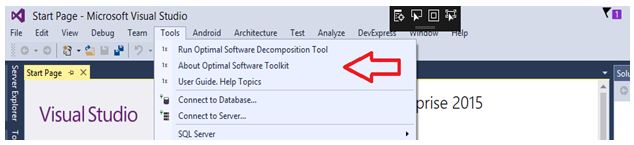
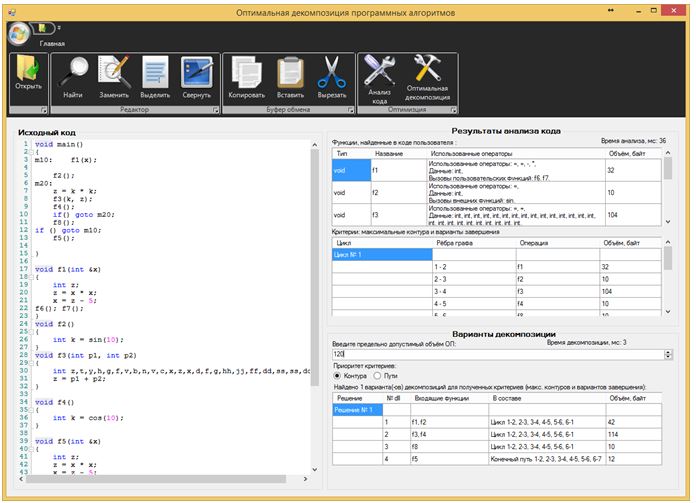
Результатом решения задачи (3) являются оптимальная стратегия размещения функция в подсистемах В общем случае, решение задач (1), (3) требует использования различного рода комбинаторных [20] алгоритмов, имеющих переборный характер, и, соответственно, высокую вычислительную сложность. Однако, экспериментальное исследование входных данных, а именно времени, затрачиваемого программой на обслуживание внешних носителей в момент загрузки подсистемы в быструю память, позволило выявить частный случай, наиболее распространенный на практике, позволяющий применить иные, более эффективные, методы решения по сравнению с комбинаторными. Время чтения данных с внешнего носителя, включает две составляющие: 1) Время позиционирования устройства (поиск данных, перемещение устройства чтения в нужную позицию, перевод в режим повышенного энергопотребления, «раскрутка» — для устройств типа «винчестер») — это значение является величиной постоянной. 2) Время непосредственно чтения данных — происходит с линейной скоростью и, соответственно, прямо пропорционально объему считываемого блока данных. Таким образом время загрузки программной системы, разбитой на N подсистем равно: где N — количество подсистем. S — скорость чтения с устройства чтения. Очевидно, что накладные расходы на декомпозицию по сравнению с идеальными условиями (когда оперативной памяти достаточно и программная система может быть полностью помещена в оперативную память и задача декомпозиции неактуальна) могут быть выражены с помощью суммы: Можно сделать вывод что выигрыш, получаемый при выборе оптимальной декомпозиции в задачах (1), (3) зависит только от числа подсистем и всегда равен: где Учитывая (7), в задачах (1), (3) можно принять значения входных данных Далее будет предложен эффективный метод решения, основанный на выводах (7), (8). 2.2. Методы решения оптимизационных задач Использование свойства (8) позволяет предложить быстрый алгоритм (Алгоритм 1) декомпозиции функций на линейных участках программ (пример решения подобной задачи был рассмотрен в предыдущей главе). В следующем алгоритме используются обозначения: V — верхняя граница размера каждой подсистемы (объем доступной оперативной памяти) — является частью входных данных. Алгоритм 1. Процесс решения задачи оптимальной декомпозиции пользовательской программной системы окончательно можно представить в виде следующих этапов: Алгоритм 2. 1) На графе, описывающем алгоритм пользователя, выполняется поиск максимального по времени работы контура 2) Размеры функций, составляющих контур 3) На графе, описывающем алгоритм пользователя, выполняется поиск максимального по времени варианта завершения программы 4) Размеры функций, составляющих максимальный путь 5) Конец алгоритма. Методы поиска контуров и экстремальных путей (шаги 1 и 3) используют подходы, изложенные в работе [3]. Алгоритмы 1 и 2 не содержат переборных составляющих, таким образом благодаря сведению исходных данных к условию (8) удалось избежать комбинаторных методов, крайне требовательных к вычислительным ресурсам ЭВМ. Описание программной реализации предложенных подходов к решению задач приводится в следующей главе. 2.3. Описание программной реализации. Оптимизационное дополнение (Add-In) для Microsoft Visual Studio Практическим результатом исследований стал программный пакет, разработанный на основе рассмотренных в предыдущих главах подходов. Продукт состоит из двух приложений: 1) Модуль «CodeOptimizationToolsExtension.vsix» — представляет собой дополнение (Add-In) к популярной среде MS Visual Studio. Технология VSIX позволяет модифицировать стандартный интерфейс среды разработки, добавляя собственные элементы управления (меню, панели инструментов и т.д.). VSIX-модуль используется для добавления новых пунктов в меню «Tools» среды Visual Studio (рис.2): 2) Приложение «OptimalDecomposition.exe» — представляющее собой средство поиска оптимального состава подсистем (рис.3).
Рис. 2. Новые пункты в меню «Tools» MS Visual Studio 2015. Первый пункт меню — «Run Optimal Software Decomposition Tool» выполняет запуск непосредственно модуля декомпозиции, автоматически подгружая в него код активного файла, открытого в этот момент в Visual Studio. Рис.3. Окно модуля оптимальной декомпозиции. Второй пункт меню — «About Optimal Software Toolkit», — содержит краткие сведения о программе (рис.4).
Рис.4. Окно с краткими сведениями о программе. Пункт меню «User Guide. Help Topics» вызывает руководство пользователя, включающее описание возможностей программы, технические характеристики, требования к системе, а также подробную инструкцию по эксплуатации (рис.5). Инструкция составлена в формате «RTF» и расположена в файле «UserGuideOPT.rtf». Рис.5. Руководство пользователя. Процесс оптимизации исходного кода включает в себя следующие шаги: 1) Загрузка исходного кода — возможна двумя способами : а) Автоматически при выборе пункта «Run Optimal Software Decomposition Tool» в меню «Tools» главного окна MS Visual Studio. Если в этот момент имеется хотя бы одно активное окно, содержащее исходный код, то будет выполнено автоматическое копирование соответствующего текста и окно инструмента декомпозиции (рис.2) появится с предварительно заполненным элементом редактирования в своей левой области. б) Второй способ загрузки документа заключается в использовании кнопки «Открыть» вверху окна (первая кнопка панели инструментов) 2) Анализ исходного кода — является первым и обязательным этапом оптимизации. Для его запуска необходимо воспользоваться кнопкой «Анализ» на панели (в группе «Оптимизации» в правой области). Результаты анализа отражаются в таблицах «список функций» и «Критерии». 3) Вычисление оптимальной стратегии декомпозиции — выполняется с помощью кнопки «Оптимальная декомпозиция». Состав каждого модуля указывается в третьей таблице «Варианты декомпозиции». Полученные результаты являются руководством для разработчика по оптимальному размещению функций в подсистемах (например, в DLL-библиотеках в ОС Windows). Практическая реализация полученных с помощью разработанного программного продукта рекомендаций зависит от версии ОС и реализованных в ней технологий поддержки модульности. В частности, в ОС Windows, декомпозиция исходного варианта кода на DLL-библиотеки будет заключаться в замене вызовов функций, помещенных в библиотеку, обращением к библиотеке с помощью пары API-функций «LoadLibrary» / «FreeLibrary», а также вызовом «GetProcAddress» для получения адреса экспортируемых функций. 3. Результаты и обсуждение В результате проведенных исследований разработаны модели поиска оптимального функционального состава подсистем, минимизирующего время работы с медленной внешней памятью и, соответственно, улучшающего производительность пользовательского кода. На основе предложенных моделей создан программный продукт, реализующий описанные в работе подходы. Детальный анализ процессов, происходящих при загрузке подсистем позволил уточнить параметры входных данных и применить эффективные производительные методы оптимизации, отойдя при этом от традиционных комбинаторных подходов, применяемых в общем случае, что, в свою очередь, фактически убирает ограничение на размерность входных данных (объем исходного кода). Проведенные замеры показали, что накладные расходы времени связаны с работой функции «LoadLibrary», что очевидно связано с тем, что наиболее медленные операции позиционирования, а также подготовки виртуальной памяти для размещения загружаемого модуля происходят именно в момент вызова этой функции. Выбранная модель программной реализации — надстройка «Add-In» к среде «Microsoft Visual Studio», — позволила обойти ряд технических вопросов (напрмер, проблема валидации пользовательского кода), не находящихся в центре данного исследования, но являющихся технологически необходимыми. Кроме того, совместимость с популярной средой «Microsoft Visual Studio», являющейся фактическим стандартом для разработчиков на платформе Windows, также облегчает переход на новые оптимизационные технологии широкому кругу разработчиков. 4. Выводы Полученные в ходе первого года исследований результаты позволили создать теоретический и практический задел для продолжения работ, направленных на развитие технологии глобальной оптимизации программных кодов. Математические модели в своей основе используют универсальный подход к выделению «важных» (с точки зрения выбранного критерия качества) участков программ, который может быть распространен на другие способы оптимизационных преобразований. В частности, по плану второго этапа планируется к реализации ряд инструментов на базе методов так называемого «экстремального программирования» (т.е. таких, которые позволяют улучшить выбранный пользователем критерий качества программы за счет использования дополнительного объема того или иного типа вычислительных ресурсов). Библиографический список 1.Касьянов В. Н. Практический подход к оптимизации программ. // Препринт /ВЦ СО АН СССР.—Новосибирск, 1978.— № 135,— 43 с. References 1.Kas’yanov V. N. Prakticheskij podhod k optimizacii programm. // Preprint /VC SO AN SSSR.—Novosibirsk, 1978.— № 135,— 43 p. |

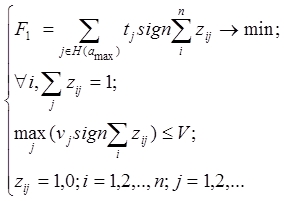 (1)
(1) 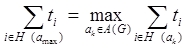 (2)
(2) 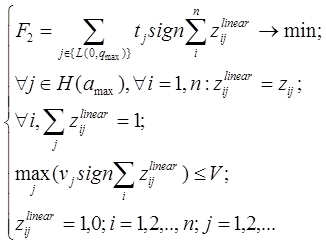 (3)
(3) 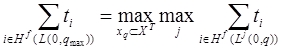 (4)
(4) 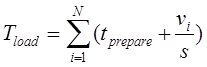 (5)
(5) 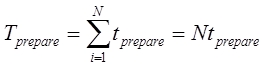 (6)
(6)