Алгоритм моделирования орбит системы объектов дифференциальным уравнением кривых второго порядка
The Algorithm Simulation of the Orbits of Objects Differential Equation Second-Order CurvesУДК 51-71 11.04.2017 Выходные сведения: Авторы: Authors: Ключевые слова: Keyword: Аннотация: В статье описан алгоритм вычисления траекторий движения тел по кривым второго порядка, через связный граф. Граф построен на решении дифференциального уравнения кривых второго порядка, теоремы центра масс, перехода от последовательного ряда относительных координат к единой системе координат. Также предложены задачи на вращение тела вокруг своей оси, за счёт изменения координат центра массы тела, под действием теплового излучения второго тела. Annotation: In this paper we consider the algorithm for calculation of motion of bodies, using the coherent graph. The graph is built through solving a differential equation of second order curves, using theorem of the center of mass and transition from a consecutive number of relative coordinates to general system of coordinates. We consider also some problems of the origin of body rotation under the influence of the thermal radiation from the second body. Содержание Часть I § 1. Алгоритм § 2. Возникновение и необходимость вращения планет вокруг своей оси Часть II § 1. Вывод дифференциального уравнения кривых второго порядка
Часть I: § 1. Алгоритм Пренебрегая размерами тел, будем пользоваться термином материальные точки, или просто точки. Дифференциальное уравнение кривых второго: a(t) – угол между большой осью и радиусом от точки до фокуса. e – эксцентриситет.
Масса первой точки много меньше массы второй. Максимальное и минимальное расстояние между точками известно, вторая точка находится в одном из фокусов эллипса, тогда движение первой точки можно вычислить по формуле (1).
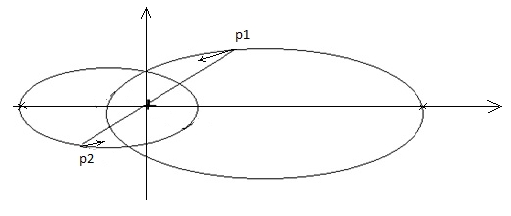
Массы точек p1, p2 сопоставимы и известны m1,m2. Известно максимальное и минимальное расстояние между точками – a12,b12. Рис. 1 Центр масс совместим с началом координат. Вычислим полуоси эллипсов – a1, b1, a2, b2: Из системы уравнений (2) – (5) находим: Вычисляем эксцентриситеты. Точки движутся синхронно, иначе столкнутся. Рассчитываем движение точек по формуле (1).
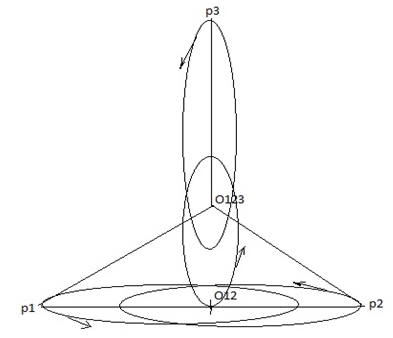
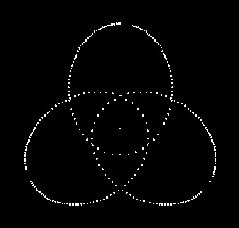
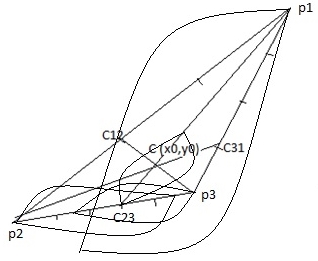
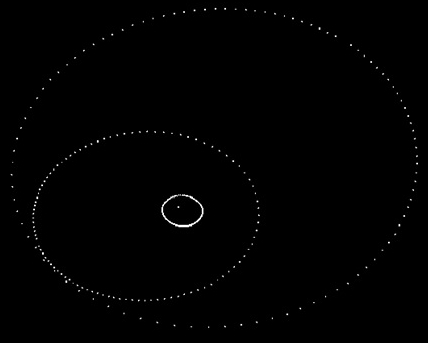
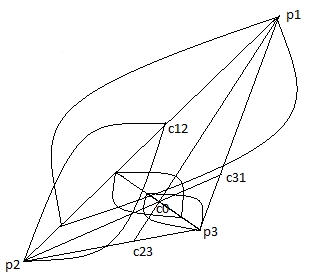
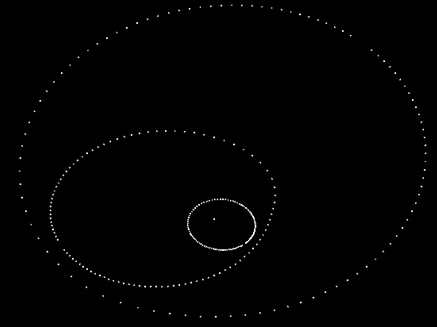
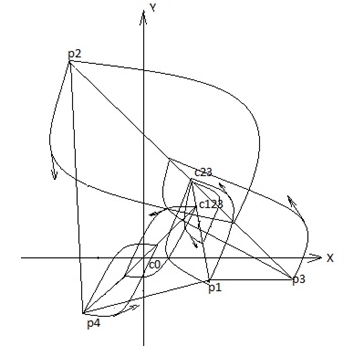
a) Масса точек m1,m2, m3 известны. Система точек имеет общий центр вращения. Совместим общий центр точек с началом координат. b) Максимальное и минимальное расстояние между точками известно. c) Точки вращаются по своим орбитам парно синхронно. Алгоритм Вычисляем орбиты данных точек. Орбита каждой точки есть сумма орбит её графа. Из исходных данных вычисляем координаты точек относительно общего центр вращения. Общий центр вращения считаем неподвижным. Формируется связный граф до общего центра вращения, через промежуточные центры вращения пар, в которых участвовала данная точка. a) Задать начальную точку графа. b) Другие точки группируются непересекающимися парами. c) Вычислить координаты центров вращения пар точек и присвоить центрам массу равную сумме масс соответствующей пары точек. d) Для каждой пары проводится вычисление по алгоритму пункта 2. Движение двух точек вокруг общего центра масс. e) Получили новую систему точек: начальная точка + центры масс пар точек для нечётного числа, начальная точка + центры масс пар точек + 1 для чётного числа, заданной системы точек. Повторить пункты c), d), e) для новой системы точек. f) Пункт f) повторить в цикле, пока не останется система из двух точек, начальная точка + центр масс остальных изначально заданных точек. Выполнить последний раз пункт 2. g) Для каждой точки выполнить сложение координат относительных систем отсчёта. Углы, угловые скорости, угловые ускорения, параметрические радиусы вычисляются по формуле (1) программой ZweiObjekte1Winkel.exe. Углы, угловые скорости, угловые ускорения, параметрические радиусы записываются в файлы ellpi*.txt. Примеры: Все точки имеют период вращения T = 1. Задаётся точность вычисления – число интервалов времени на траектории (в примерах вычисляется 100 интервалов на каждом эллипсе). Интервал равен T/100 = 0.01. Пример 1. Рис. 1. Две точки. Видео ролик Objectes2.swf.html. В следующих примерах для упрощения расчетов полагаем, что на всех эллипсах движение против часовой стрелки и все эллипсы имеют одинаковый эксцентриситет. Пример 2. Рис. 2 Рис. 2 Имеем три объекта равной массы m1:m2:m3 = 1:1:1. Все орбиты – эллипсы. Расстояние между объектами задано, p1p2 = p2p3 = p3p1 = 8. Задан эксцентриситет e = 0.6. Строим граф орбит. Центры вращения вычисляются по правилу центров масс. Имеем три варианта: (p1(p2,p3)), (p2(p1,p3)), (p3(p1,p2)). Ввиду симметрии системы, графы эквивалентны. Возьмём граф (p3(p1,p2)) = (p3,O12). Знак равенства означает, что каждое звено графа заменено центром масс точек звена, например (p1,p2) = O12. Вычисления начинаются с внутренних скобок. Вычисляем большие и малые оси. Вычисляем скорости движения объектов в точках орбит с заданным интервалом по времени. Полученные углы, угловые скорости, угловые ускорения, параметрические радиусы записаны в файлы ellpi*.txt. Программа Objecte3-1-1-1 вычисляет орбиты объектов по описанному алгоритму. Видеоролик Objectes3-1-1-1.swf.html. Исполняемый файл Objecte3-1-1-1.exe, файлы данных ellpi*.txt в папке Objectes3-1-1-1. Видеоролики в папке ObjectesVideosHTML. В виду симметрии все три объекта должны иметь одинаковые орбиты и иметь симметрию относительно центра вращения. Что и видно на рис. 3. Рис. 3 Пример 3. Рис. 4. Рис. 4 Зададим массы m1:m2:m3 = 1:2:3, Имеем координаты объектов относительно центра вращения. Все орбиты – эллипсы. Задаём эксцентриситет e = 0.3. Строим граф орбит. Имеем три варианта: (p1(p2,p3)), (p2(p1,p3)), (p3(p1,p2)). Возьмём граф (p1(p2,p3)) = (p1,c23). Вычисляем большие и малые оси. Все объекты имеют период вращения T = 1, этим обеспечивается синхронность движения. Вычисляем скорости движения объектов в точках орбит с шагом по времени 0.01*T. Данные углов, угловых скоростей, угловых ускорений, параметрических радиусов находятся в файлах ellpi*.txt. [11, 12, 13] Программа Objecte3-1-2-3 вычисляет орбиты объектов по описанному алгоритму. Видеоролик Objectes3-1-2-3.swf.html. Исполняемый файл Objecte3-1-2-3.exe, файлы данных ellpi*.txt в папке Objectes3-1-2-3. Рис. 5. Орбиты объектов примера 3. Пример 3а. Рис. 6. Рис. 6 Повторим пример 3 с другим графом орбит (p3(p1,p2)) = ((p3,c12)). Данные углов, угловых скоростей, угловых ускорений, параметрических радиусов находятся в файлах ellpi*.txt. Программа Objecte3-1-2-3a вычисляет орбиты объектов по описанному алгоритму. Видеоролик Objectes3-1-2-3a.swf.html. Исполняемый файл Objecte3-1-2-3a.exe, файлы данных ellpi*.txt в папке Objectes3-1-2-3a. Рис. 7. Орбиты объектов примера 3а. Видим, что рис. 5 и рис. 7 подобны, т.е. орбиты примеров 2 и 2а качественно схожи. Требуется найти функцию подобия графов (p1(p2,p3)) и (p3(p1,p2)). Возможно, необходимы более точные вычисления. Пример 4. Рис. 8 Рис. 8 Положим массы m1:m2:m3 = 1:2:3:4, Имеем координаты объектов относительно центра вращения. Все орбиты – эллипсы. Задаём эксцентриситет e = 0.3. Строим граф орбит. Возьмём граф (p4(p1(p2,p3))) = (p4(p1,с23))) = (р4,с123). Вычисляем большие и малые оси. Все объекты имеют период вращения T = 1, этим обеспечивается синхронность движения. Вычисляем скорости движения объектов в точках орбит с шагом по времени 0.01*T. Данные углов, угловых скоростей, угловых ускорений, параметрических радиусов находятся в файлах ellpi*.txt. Программа Objecte4-1-2-3-4 вычисляет орбиты объектов по описанному алгоритму. Видеоролик Objectes4-1-2-3-4.swf.html. Исполняемый файл Objecte4-1-2-4.exe, файлы данных ellpi*.txt в папке Objectes4-1-2-3-4. Рис 9. Объекты – p1, p2, p3, p4. Центры вращения – c0, c12, c123. Пример 5. Смоделируем вращение двух одинаковых тел вокруг третьего, подобных спутникам Сатурна Янусу и Эпиметею. Положим период вращения вокруг центрального тела, равен 1году, за 1 период 4 пересечения орбит. Получаем 3-х кратное взаимное вращение, вокруг центра вращения двух тел (Януса и Эпиметея). Рис 10. Пример 5а. Обратные условия, задаем 5 вращений первых двух тел относительно друг друга (подобно Луна с Землёй). Получаем 8 пересечений орбит за 1 период вращения вокруг центрального тела 3. 6 периодов – 10 пересечений. N периодов = 2N-2 пересечений орбит.
И так далее для заданного числа тел получаем орбиты относительно общего центра вращения. Данные углов, угловых скоростей, угловых ускорений, параметрических радиусов находятся в файлах ellpi*.txt. Программа Pendel3_1_2GraphOpenGl вычисляет орбиты объектов по описанному алгоритму. Видеоролик Ja-E_4p.swf.html. Исполняемый файл Pendel3_1_2GraphOpenGl.exe, файлы данных ellpi*.txt в папке Pendel3_1_2GraphOpenGl. Заключение:
Математика a) Выявить и доказать свойства уравнения (1). b) Доказать эквивалентность (подобие) графов системы при различных начальных точках. Примеры 3 и 3а. Астрономия a) Проверить и доказать (не) соответствие с реальными системам объектов, т.е. правомочность алгоритма. b) Для движения точки по эллипсу в одном направлении, из уравнения (1) следует необходимость прецессии, так как отсутствие прецессии приводит к неопределённости продолжения движения в точках пересечения большой оси с периметром эллипса. Данное уравнение позволяет рассчитывать траекторию движения тела по эллипсу, учитывая прецессию. В примерах вычисление орбит производилось без учёта прецессии. Обозначим прецессию перицентра буквой dp, тогда интегрируем уравнение (14) от 0 до π+dp. В результате вычисления также получаем прецессию апоцентра da. При следующем цикле смещаем 0 на величину da.
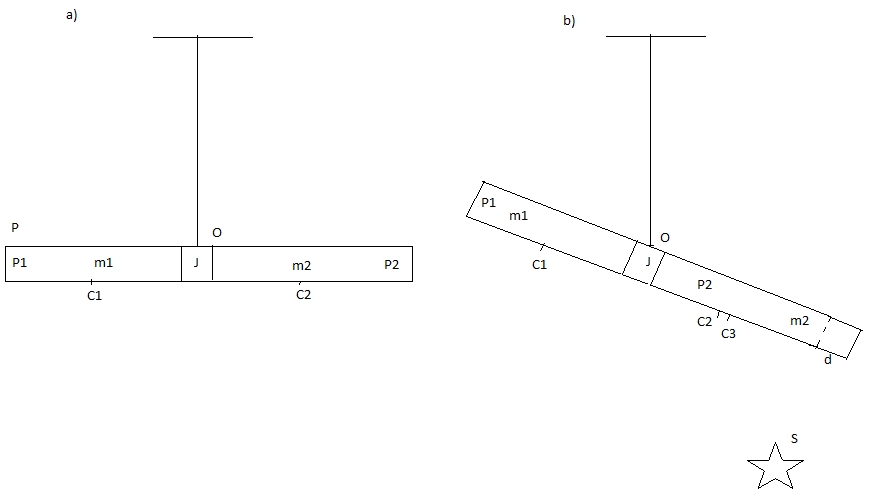
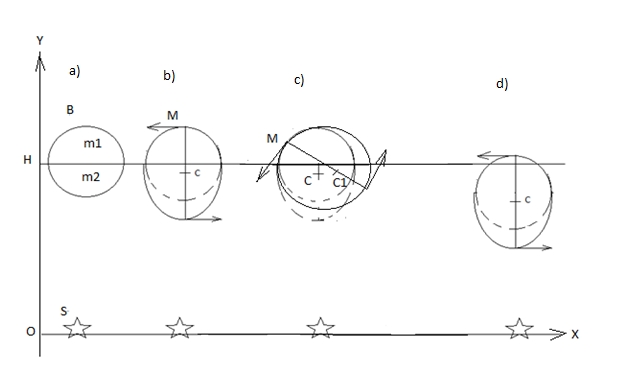
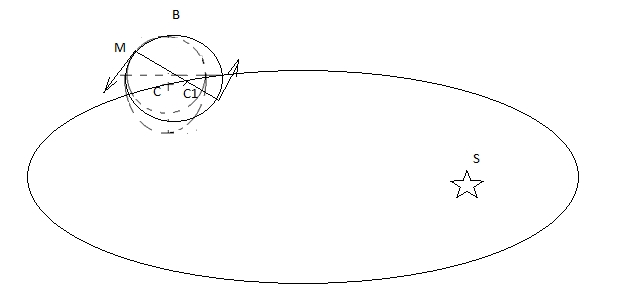
Физика. физическая и компьютерная модели движения тел, демонстрирующие данный алгоритм орбит, будут описаны в следующей статье. Дополнения: Все видеоролики находятся по адресу fayloobmennik.net/4823487 § 2. Возникновение и необходимость вращения планет вокруг своей оси Продемонстрируем влияние температурного расширения на изменение центра массы. На Земле центр массы совпадает с центром тяжести. Возьмём две равных, по массе и длине, металлических балки P1 и P2. m1 = m2, l1 = l2. Соединим их через теплоизолирующую прокладку J. Получили балку Р. Подвесим балку Р за центр О. Рис.11, часть а). Под Р2 поместим источник тепла S. Под действием тепла длина Р2 увеличится на величину d. Рис.1, часть b). Центр массы балки Р2 сместится из точки С2 в С3. Так как (О,С3) больше (О,С1), образуется крутящий момент М. Естественно, что направление момента М в условиях Земли предсказуемо. Рис. 11 Поместим балку Р в невесомости и повторим эксперимент. В нагретом конце балки колебание молекул более интенсивно, чем в противоположном. Можно предположить возникновение момента вращения под действием тепла. Если гипотеза верна, то можно предложить следующие задачи: Задача 1. В невесомости, в вакууме, в системе координат XY, поместим тело В на расстоянии ОН от оси Х. Для простоты положим, что В твёрдый однородный шар массой m. Из центра В опустим перпендикуляр на ось Х и в точку пересечения поместим источник тепла тело S. Температура пространства (Т) меньше температуры тела S (T1), T < T1. На тело В не действуют ни какие силы, кроме теплового излучения от тела S. Рис.12. Рис. 12 Имеем m1 = m2, m1 + m2 = m. Под действием тепла, ближняя к S, сторона тела В расшириться. В следствии чего центр массы тела В сместиться на Δy в направлении к S. Также под действием тепла в теле возникнет крутящийся момент М. Здесь неважно в какую сторону он повернёт тело В. Положим что поворот произошёл в +Х на угол α. Центр массы тела В сместился на Δy1 и Δх. Противоположная сторона В остывает. Источник S сдвигаем на Δх. Цикл повторятся, но уже с новыми координатами. Тела В и S через какой-то промежуток времени столкнутся. Задача 2. Изменим условия задачи 1. Источник тепла S неподвижен. Тело B движется по кривой второго порядка. Рис.13. Чтобы орбита была устойчивой необходимо, чтобы смещение центра массы тела В попадало на заданную кривую. Рис. 13 Предлагается найти формулы, или создать алгоритм вычисления соотношения массы тела В, коэффициентом расширения вещества тела В, интенсивности излучения тела S, и параметрами орбиты тела В. Косвенное подтверждение существование решения, это наличие вращения вокруг своей оси у планет, и отсутствие вращения вокруг своей оси у спутников планет, например у Луны. Часть II: § 1. Вывод дифференциального уравнения кривых второго порядка
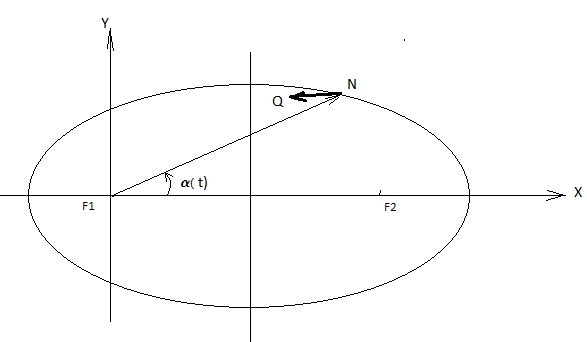
Рассматривается задача вывода дифференциального уравнения кривых второго порядка на исследовании движения материальной точки (дальше просто точка) по эллипсу под действием внешней силы [3 – 16]. Поместим точку массой m в пространство без гравитации. Условия – внешняя сила перемещает точку по кривой второго порядка. В данном случае по эллипсу, вокруг левого фокуса.
Рис.1. Движение точки по эллипсу вокруг левого фокуса N – маятник. Совместим левый фокус с началом координат, тогда (A, B – полуоси эллипса) r – радиус до левого фокуса. e – эксцентриситет эллипса Для составления дифференциальных уравнений движения изобразим силу, действующую на точку в неподвижной декартовой системе координат. Из (3) подставим (5) в (4) Координаты точки можно представить как функцию угла отклонения α(t) и функцию радиуса r(t)
Вычислим первые, и вторые производные по времени системы уравнений (7),(8) Подставим уравнения (11),(12) в уравнение (6) и перенесём всё в левую часть или Получили дифференциальное уравнение кривых второго порядка. При различных значениях эксцентриситета будет изменяться вид кривой. Заключение Одно из свойств этого уравнения постоянная секторальная скорость, что даёт возможность моделировать орбиты тел по законам Кеплера. Для движения точки по эллипсу в одном направлении, из уравнения (15) следует необходимость прецессии, так как отсутствие прецессии приводит к неопределённости продолжения движения в точках пересечения большой оси с периметром эллипса. Данное уравнение позволяет рассчитывать траекторию движения тела по эллипсу, учитывая прецессию. Несколько примеров (видеоролики) находятся по адресу: fayloobmennik.net/4823487 1. Сивухин Д. В. Общий курс физики в 5 томах, издательство МФТИ, Россия, 2005 References 1. Sivuhin D. V. Obshhij kurs fiziki v 5 tomah, izdatel’stvo MFTI, Rossija, 2005 |

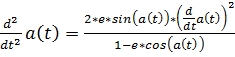 (1)
(1) 
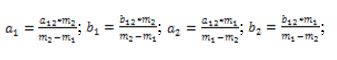



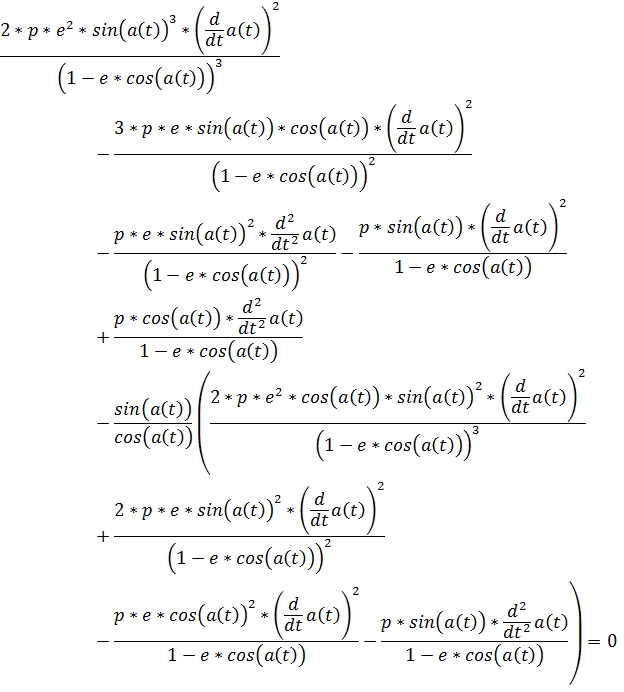
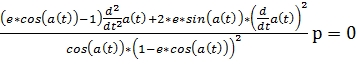 (13)
(13) 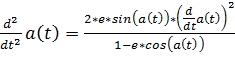 (14)
(14) 
