Экспертные системы для медицинской диагностики с применением методов теории нечетких множеств
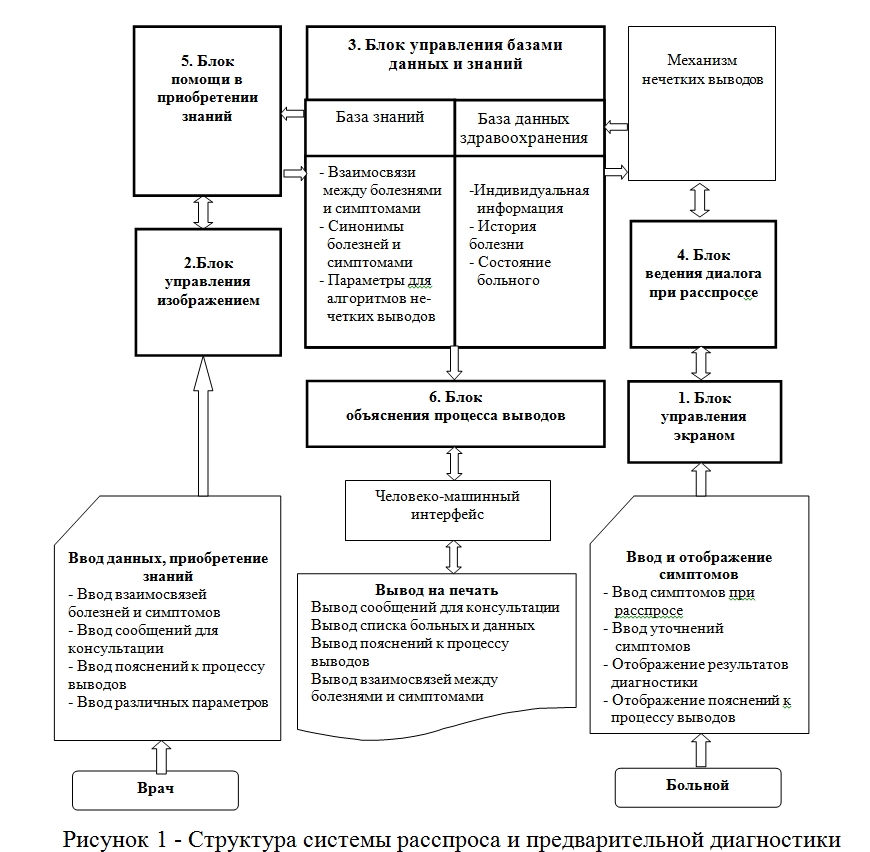
Expert systems for medical diagnostics using methods of fuzzy set theoryУДК 51.001.57 03.11.2016 Выходные сведения: Авторы: Authors: Ключевые слова: Keyword: Аннотация: На основе методов теории нечетких множеств предлагается подход к созданию экспертной системы для медицинской диагностики с учетом нечеткости исходной информации и оценок. Выделены основные проблемы при создании экспертной системы для медицинской диагностики связанные с представлением, использованием и приобретением знаний, и предложены методы их решения на основе методов теории нечетких множеств и нечеткой логики. Создана структура предлагаемой экспертной системы расспроса больных и предварительной диагностики описаны ее функциональные блоки: блок управления экраном; блок управления изображением; блок управления базами данных и знаний; блок ведения диалога при расспросе; блок помощи в приобретении знаний; блок объяснения процесса выводов. Разработана блок-схема процедуры оценки в системе расспроса и предварительной диагностики. Для описания и формализации взаимосвязи болезни и симптомов используется матрицы нечетких отношений. Дано описание алгоритма диагностики, использующего лингвистические значения истинности. Для решения проблем проведения экспертных процедур в нечеткой среде предложен эффективный метод организации и проведения экспертной оценки, учитывающий особенности человеческой процедуры оценки, знания врачей и методологию теории нечетких множеств. Таким образом, предлагается подход к созданию экспертной системы, которая может способствовать раннему обнаружению и лечению болезней благодаря активной постановке диагноза самой системой. Для обеспечения и повышения точности выводов в предлагаемой экспертной системе вводится модель, основанная на нечетком соответствии как более широком понятии. Annotation: Created structure of the proposed expert system questioning patients and preliminary diagnosis describes its functional units: the control unit screen; The image control unit; unit database management and knowledge; block dialogue with the questioning; unit aid in the acquisition of knowledge; Block explaining the conclusions of the process. A block diagram of an evaluation process in the system of questioning and preliminary diagnosis. For a description and the formalization of the relationship of the disease and symptoms is used matrices of fuzzy relations. The description of the diagnostic algorithm, using the linguistic truth values. To solve the problems of expert procedures in fuzzy environment, we propose an effective method for organizing and conducting peer review, taking into account the peculiarities of human assessment procedures, doctors knowledge and methodology of fuzzy set theory. Thus, we propose an approach to the creation of an expert system, which can contribute to early detection and treatment of diseases due to the active diagnosis of the system. In order to ensure and improve the accuracy of the conclusions in the proposed expert system is introduced a model based on fuzzy match as a broader concept. Введение. Экспертные системы (ЭС) — один из видов систем искусственного интеллекта, построенные на основе знании специалистов – экспертов получили широкое распространение и нашли практическое применение во многих отраслях, в том числе и в медицине [1–3]. К основным отличительным признакам ЭС от других компьютерных систем можно отнести [4–9]: 1) компетентность — в конкретной предметной области ЭС должна достигать того же уровня, что и эксперты — специалисты, при этом она должна пользоваться теми же эвристическими приемами, также глубоко и широко отражать предметную область; 2) глубина — экспертиза должна решать глубокие, нетривиальные и нечеткие задачи, отличающиеся сложностью, ЭС использует эвристические, творческие, неформальные методы; 3) самосознание — ЭС должна включать в себя механизм объяснения того, каким образом она приходит к решению задачи. ЭС ориентированы не на проблемы, формализация которых проста и решение которых можно найти с помощью математических моделей и алгоритмов, т.е. не на проблемы, с которыми имеют дело современные программы, а скорее на сложные проблемы, которые можно решить только с использованием знаний, полученных экспертами за долгие годы. Такие знания подбирают методом проб и ошибок, добавляя, изменяя или удаляя знания. В этом смысле использование экспертных систем в медицине имеет весьма важное значение. В процессе развития искусственного интеллекта возникли проблемы, связанные с нечеткостью исходной информации. Решение этих проблем стало возможным с разработкой теории нечетких множеств (ТНМ) [10–16]. ТНМ превратилась в методологию, разработанную в результате исследований искусственного интеллекта, прежде всего, имеет тесную связь с ЭС. К настоящему времени проведено много исследований медицинских систем, использующих нечеткие выводы. Этими исследованиями охвачены многие разделы медицины, например, фундаментальные исследования Санчеса [17], исследования Эдлессинга [18], Тадзаки [19] и др. Безусловно, в ЭС использовалось представление недостоверности фактов и правил в виде коэффициентов уверенности так, как в системе диагностики инфекционных заболеваний MYCIN. В частности, она предназначена для работы в области диагностики и лечения заражения крови и медицинских инфекции. Система ставит соответствующий диагноз, исходя из представленных ей симптомов, и рекомендует курс медикаментозного лечения любой из диагностированных инфекций. MYCIN состоит в общей сложности из 450 правил, разработанных с помощью группы по инфекционным заболеваниям Стэндфордского университета. Система MYCIN справляется с задачей путем назначения показателя определенности каждому из своих 450 правил. Поэтому можно представлять MYCIN как систему, содержащую набор правил вида «Если… то» с определенностью Р, которые предоставили люди — эксперты — и которые изложили и правила и указали свою степень доверия к каждому правилу по шкале от 1 до 10. Установив эти правила и связанные с ними показатели определенности, MYCIN идет по цепочке назад от возможного исхода, чтобы убедиться, можно ли верить такому исходу. Установив все необходимые исходные предпосылки, MYCIN формирует суждение по данному исходу, рассчитанное на основе показателей определенности, связанных со всеми правилами, которые нужно использовать. Также известно ЭС «Кардиолог», которая определяет диагноз больного по введенным симптомам, назначает курс лечения и профилактики. Операции с недостоверностью в этих системах основаны на идеях байесовской вероятности. Вероятностные выводы в настоящее время исследуются как один из методов, используемых в ЭС, но, сущность эксперта не в вероятностной природе, а в нечетких тезисах. В этой связи исследование решение проблем разработки ЭС для медицинской диагностики с применением методов ТНМ с целью повышения надежности и адекватности систем является актуальной задачей медицины и искусственного интеллекта. Материалы и методы исследования. Во многих лечебно-диагностических технологиях возможности современных компьютеров используются не в полной мере. Прежде всего, это диагностика, назначение лечебных мероприятий, прогнозирование течения заболеваний и их исходов. Можно отметить, что основными причинами недостаточно полного использования современных математических методов и компьютерных технологий в медицине являются слабо развитая техническая база, недостаточный уровень подготовки участников этих технологий, плохая оснащенность специализированными пакетами прикладных программ, сложности учета исходной нечеткой информации, представляющей собой опыт и знаний специалистов – экспертов (врачей). Большое значение имеет психологический аспект применения компьютерных приложений. Это серьезная причина, связанная с особенностями работы врача. Врач является исследователем, его работа носит творческий характер, однако он несет прямую ответственность за результат своей деятельности. Принимая решение о диагнозе или лечении, он опирается на знания и опыт – свои собственные и коллег. Очень важно при этом обоснование решения, особенно если оно подсказывается аргументировано со стороны [21], например экспертными системами. Медицинские экспертные системы позволяют врачу не только проверить собственные диагностические предположения, но и обратиться к компьютеру за консультацией в трудных диагностических случаях. Они позволяют решать задачи диагностики, дифференциальной диагностики, прогнозирования, выбора стратегии и тактики лечения и др. В области ЭС для медицинской диагностики можно выделить три проблемы: представление знаний; использование знаний; приобретение знаний. ТНМ может внести существенный вклад в решение любой из этих проблем. Для проблемы 1 главным оказывается то, что наиболее высокий уровень представления гарантирован с помощью языка, знания типа фактов, правил, оценок и другие знания врача можно представить только в форме, содержащей нечеткости. Более того, поскольку человек допускает применение неопределенностей, можно подобрать знания, которые проще использовать. В представлении знаний используются понятия нечетких множеств, но для проблемы 2 эффективнее нечеткая логика. Основным методом является метод нечетких выводов. Особенность таких выводов заключается в получении выводов из нечеткой информации с помощью знаний о нечетких правилах, но это же можно сказать и о применении знаний экспертами. Применение знаний не ограничивается только выводами. Кроме выводов серьезной проблемой являются оценки и суждения. В качестве моделей оценок и суждений экспертов на основе эмпирических знаний эффективны идеи нечетких изменений и нечеткого интегрирования. При решении проблемы 3 в первую очередь надо научиться извлекать эмпирические знания экспертов (врачей). При этом часть таких знаний можно передать только с помощью нечетких слов, поэтому необходима нечеткая интерпретация знаний. Благодаря введению нечеткой классификации знаний типа правил по условиям их применения становится возможным гибкое приобретение знаний эксперта. Второй по значению задачей является поиск методов извлечения знаний, причем не только непосредственно со слов врача — эксперта, но и косвенно, путем наблюдения за действиями эксперта или даже без эксперта через эксперименты и обучение. В последнем случае для сбора данных и информации так, как это делает эксперт, можно использовать нечеткую логику. Другими словами, выполняют сбор качественной информации типа «Если х есть определенные симптомы, то у есть определенные болезни». Благодаря использованию нечеткого представления можно определить суть работы эксперта. Таким образом, основными методами исследования и используемые в данной работе являются методы экспертных оценок и теории нечетких множеств. Результаты и обсуждение. В настоящее время в условиях повышенных требований населения к здравоохранению и изменения характера болезней раннее обнаружение болезней людей в медицинских учреждениях является важной задачей медицины, которую можно успешно решать с применением ЭС, разработанной с применением методов ТНМ. Цель предлагаемой нами системы — способствовать раннему обнаружению и лечению болезней благодаря активной постановке диагноза самой системой. Особенность системы — выполнение комплексных выводов и диагностики с помощью блока нечетких выводов, написанного на современном средстве программирования (Delphi) и знаний специалистов – экспертов (врачи, медицинский персонал), организованных в виде матриц. Рассмотрим разработанную структуру (рисунок 1) и функциональных блоков [22] предлагаемой системы расспроса больных и предварительной диагностики: 1. Блок управления экраном обеспечивает ввод исходной информации и вывод результатов в отдельные поля экрана, состоит из прикладного интерфейса, подпрограмм управления экраном, обработки и доступа к полям и других подпрограмм; 2. Блок управления изображением позволяет зрительно представлять больные органы во время расспроса и вводить их на нужное место с помощью «мыши»; 3. Блок управления базами данных и знаний позволяет эффективно использовать данных и знания путем независимого доступа к ним из механизма выводов, а также позволяет использовать данные здравоохранения независимо от данных, полученных при расспросе; 4. Блок ведения диалога при расспросе представляет собой программу для ввода в режиме диалога симптомов и их степени, о которых говорит больной, и получения результатов диагностики (состоит из группы подпрограмм для ведения расспроса, отображения, выводов, проверки симптомов и обработки ошибок); 5. Блок помощи в приобретении знаний предназначен для ввода знаний от врачей и других экспертов и их пакетной обработки. (подпрограммы для регистрации взаимосвязи симптомов и болезней, сообщений, параметров, отображения входных сообщений, проверки базы знаний и других операций): 6. Блок объяснения процесса выводов выполняет отображение результатов и печать сведений, поясняющих, как система пришла к данному выводу. Формирование данных и знаний для выводов. Традиционная процедура расспроса врачом больного состоит в следующем: больной рассказывает врачу о своих субъективных симптомах, врач выделяет среди них наиболее существенные с учетом близости симптомов одной из болезней, используя при этом фундаментальные медицинские знания и собственный опыт, затем более детально расспрашивает о симптомах, связанных с вероятной болезнью, и выдает заключение. В качестве знаний в данном случае необходимы общие взаимосвязи между болезнями и симптомами, кроме того, очевидно, необходима некоторая мера такой связи как для болезни с точки зрения ее симптомов, так и для симптомов с точки зрения болезни. С целью применения здесь методов ТНМ рассмотрим простуду и кашель. В этом случае представление знаний будет следующим: 1) простуда и кашель взаимосвязаны (степень истинности = 0,9); 2) если есть кашель, то налицо простуда (степень истинности = 0,8); 3) при простуде возможен кашель (степень истинности = 0,6). Степень истинности здесь означает достоверность взаимосвязи, т.е значения функции принадлежности. При выводах с помощью формул нечетких отношений, остается проблема, связанная со способом задания числовых значений матрицы отношений R: какая степень истинности наиболее соответствует модельному представлению? На практике использование операции максимум — минимум иногда приводит к слишком грубым значениям истинности по сравнению со свойствами объектов, и в этом смысле точность выводов снижается. Поэтому в данной системе благодаря введению модели, основанной на нечетком соответствии как более широком понятии, получены адекватные и гибкие выводы. Учитывая сказанное выше, установим тезисы для адаптации знаний к нечетким выводам. Обозначим через X и Y соответственно множество всех болезней и множество всех симптомов: Болезни Каждый из этих тезисов включает недостоверность, и в этом смысле их можно считать нечеткими множествами. Кроме того, установим следующие тезисы Pj, Pij, образованные из введенных выше тезисов: где → — импликация, OR — дизъюнкция, & — конъюнкция. Другими словами, пусть Pj- достоверность утверждения «Если есть симптом Bj, то на основании взаимосвязи Rij между болезнями и симптомами проявляется по крайней мере болезнь Аj», а Pij — достоверность утверждения «Если на основании взаимосвязи Rij между болезнями и симптомами проявляется болезнь Ai, то есть симптом Bj». Будем считать тезисы Rij, Pj, Pij знаниями для выводов. При этом можно предсказать, что достоверность Pj в общем случае довольно высокая. Однако симптом мог наблюдаться ошибочно, поэтому Pj не может быть абсолютно достоверным. В общем случае Pij зависит от внимательности человека и условий наблюдения, и поэтому достоверность Рj выше достоверности Pij. Приведем конкретные примеры Rij (таблица 1). Достоверности Rij, Pj, Pij выражены в терм-множества – в форме лингвистических значений истинности (ЛЗИ): VT — Очень правдивое; RT — Довольно правдивое; РТ — Возможно, правдивое; а также могут быть PF — Возможно, ложное; RF — Довольно ложное; VF — Очень ложное; UN – Неизвестное. Рассмотрим алгоритм диагностики. Как видно из приведенного примера информация, полученная от врача и больного включает нечеткость, выраженную через ЛЗИ. Для вычислений необходимо преобразовать эти значения в числовые значения истинности (ЧЗИ). Для их количественной оценки используются функции принадлежности. Таблица 1 — Пример взаимосвязи болезни и симптомов (Rij) для болезни почек
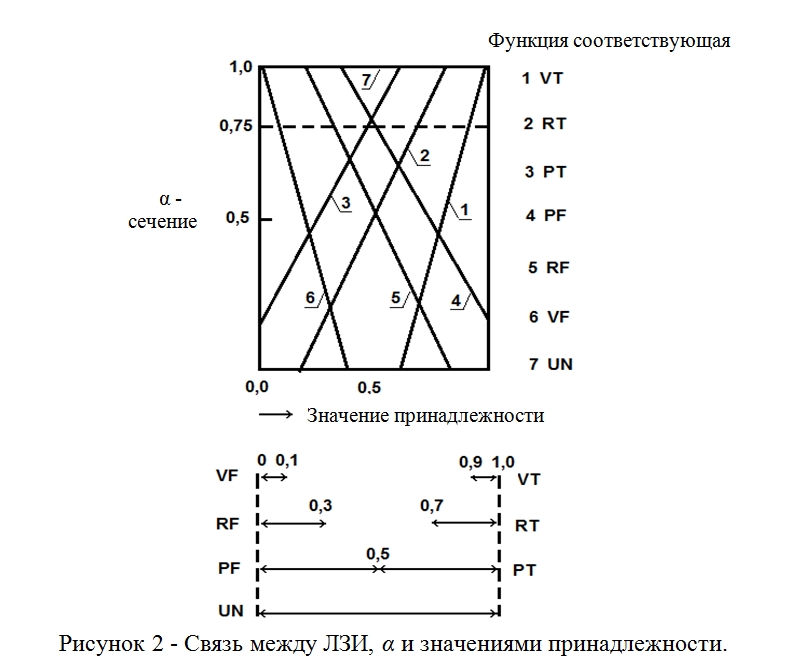
В предлагаемой ЭС такие понятия, как «немного», «очень» для симптомов и «часто», «вероятно» и др. для взаимосвязи между болезнями и симптомами, представлены ЛЗИ (семь уровней). При этом необходимо установить, каким образом выбирать по функции принадлежности каждого ЛЗИ значения принадлежности. Такие значения назовем α-сечением, а значение, выбранное для А, обозначим Аα. Обычно Аα имеет одно значение, но в целях сохранения нечеткости в словах более естественно использовать интервал значений, например для ЛЗИ «UN» (неизвестное) введем интервал [0,1]. Таким образом, будем задавать интервал значений принадлежности для всех ЛЗИ, т.е. Связь между ЛЗИ, α-сечением и значениями принадлежности показана на рисунке 2. В системе создается база данных, в которой все функции принадлежности и α-сечение являются координатами, константами и другими параметрами. Алгоритм выводов следует из формул (2) и (3). При этом предполагается, что Pj, Рij — нечеткие подмножества множества V ЛЗИ, т.е. очень правдивые и выпуклые подмножества. Если применить к формулам (2) и (3) нечеткие правила «модус поненс» и «модус толленс», то получатся следующие взаимосвязи между болезнями и симптомами: для где ┐ означает отрицание в нечеткой логике, l указывает нижнюю границу. Зададим наблюдаемые симптомы Вj — и знания Pj, Pij, Rij и обнаружим все болезни {Ai}. Ai можно получить, найдя общее решение формул (4) и (5). При этом достоверности знаний Pαj, Pαij, Bαj можно определить через интервал их значений ([нижнее значение, верхнее значение]) следующим образом: Кроме того, определим расстояние между симптомом и знаниями следующим образом:
Метод организации и проведения экспертной оценки в нечеткой среде. При организации и проведении экспертной оценки с участием врачей и пациентов возникает ряд проблем, связанных с особенностью человеческой процедуры оценки. Для решения этих проблем нами предлагается применить при организации и проведении процедур экспертных оценок в этих условиях методологию теории нечетких множеств. Разрабатываемый метод экспертной оценки при наличии нечетких факторов основывается на использования мнений экспертов и теории нечетких множеств. Разработанный нами метод организации и проведения экспертной оценки в нечеткой среде состоит из следующих пунктов (этапов): 1. Категоризация объекта оценки, классов задач и операций; 2. Выбор класса квалификаторов (терм-множество, значения лингвистических переменных), адекватных объекту оценки и классу операций, определить лингвистических значений истинности; 3. Выбор типа шкал, описывающих объект и задачи, определить числовых значений истинности; 4. Определение способа оценки для медицинской диагностики и проведение оценки; 5. На основе результатов проведенной оценки составляется базы знаний в виде «Если есть симптомы Bi, то на основании взаимосвязи Rij между болезнями и симптомами проявляется болезнь Аj»,. 6. Проверка на субъективную совместимость признаков и их совокупности (соответствие интуитивному образу объекта). Так как, при оценке участвует группа экспертов, необходимо определить степени согласованности их мнений. Если мнение экспертов в основном совпадает, т.е. значения дисперсионного коэффициента конкордации wблизки к 1 (например, 0,90≤w≤1), переход к пункту 8; 7. Если не выполняется условие 0,90≤w≤1, т.е. когда мнения экспертов не совпадают, им представляется возможность ознакомиться с ответами других экспертов, проанализировать и откорректировать свои предыдущие оценки, т.е. цикл экспертной процедуры повторяется, начиная с пункта 2. В этом пункте можно применить метод Дельфи (Delphi). 8. Построение функции принадлежности нечетких показателей и оценок, переход к обработке полученных результатов. 9. Для получения конечных результатов полученная информация обрабатывается методами теории нечетких множеств, что позволяет построить лингвистическую модель, которая правильно проводит медицинскую диагностику. В основе этого метода лежит совокупность следующих основных факторов: особенности задачи, класса нечетких категорий, способа формирования шкал, способа опроса экспертов и обработки полученной нечеткой информации. Приведем описание и пояснение к основным пунктам предложенной методики. В пункте 1 выполняется категоризация объекта оценки, классов задач медицинской диагностики и операций, т.е. организаторами экспертной оценки и экспертами производится изучение задачи диагностики, подлежащего оценке, ставится задача перед экспертами и определяется процедура и метод проведения экспертизы. Следует отметить, что во многих случаях наиболее удобным и эффективным методом проведения экспертных оценок является метод Дельфи. В пункте 2 производится выбор класса квалификаторов, т.е. определяется терм-множество — значения лингвистических переменных, адекватных объекту оценки и классу операций. Для этого выбираются наиболее информативные показатели (симптомы лингвистических значений истинности), которые правильно описывают задачу медицинской диагностики. Для удобства диапазоны изменения ЛЗП задаются в виде отрезков, с указанием минимального ( В пункте 3 осуществляется выбор типа шкал, описывающих решаемую задачу диагностик. Определяются параметры болезни и симптомов, которые подлежать оценке, а также интервалы и шкалы их оценки. В пункте 4 определяется способ оценки показателей симптомов и их взаимосвязи, например, некоторых параметров эксперты могут оценить количественно или по балльной шкале, а некоторые параметры и их взаимосвязь оценивается качественно (словесно), т.е в нечеткой среде. В пункте 5 базы знаний составляются с применением модели продукционных правил вывода: «Если … то», «Если … то … иначе». Результаты выполнения этого этапа удобно оформить в виде матрицы нечетких отношений, например в виде таблицы взаимосвязи симптомов и болезней. В пункте 6 осуществляется проверка на субъективную совместимость признаков и их совокупности, определяется насколько согласовано мнение экспертов (врачей, специалистов), участвующих в оценке. Если мнение экспертов в основном совпадает, т.е. значения дисперсионного коэффициента конкордации wблизки к 1 (например, 0,90≤w≤1), переход к пункту 8; Для проверки на субъективную совместимость оценки экспертов вычисляется коэффициент конкордации (согласия) по формуле:
где Sij — сумма ранговых оценок по каждому свойству; Если мнение экспертов не совпадает, т.е. не выполняется условие 0,90≤w≤1 (пункт 10), экспертам представляется возможность ознакомиться с ответами других экспертов, проанализировать и откорректировать свои предыдущие оценки или обосновать свой вариант оценки, т.е. цикл экспертной процедуры повторяется, начиная с пункта 2., т.е реализуются идеи метода Дельфи. Построение функции принадлежности нечетких показателей, оценок (пункт 8) является одним из основных этапов при решении задач диагностики с применением методов теории нечетких множеств [23,24]. Основным способом восстановления аналитического вида этой функции является графическое построение кривой степени принадлежности того или иного показателя соответствующему нечеткому множеству. На основе полученного графика подбирается такой вид функции, который наилучшим образом его аппроксимирует. После этого идентифицируются параметры выбранной функции [25]. Существуют другие альтернативные методы построения функции принадлежности, основанные на использования нечеткой статистики и подбора кривой функции принадлежности. На основе опыта исследования задач оценки нечетких показателей и оценок при решении задач диагностики и других аналогичных задач в нечеткой среде нами предлагается следующая структура функции принадлежности экспоненциального типа в следующем виде: где Лингвистическая модель решаемой задачи строится по результатам обработки экспертной информации. Для удобства ее можно оформить в виде таблицы, где словесно (нечетко) указаны различные значения входных параметров Нечеткие отображения для кванта р можно определить следующим образом: Для синтеза нечетких моделей можно применить композиционного правила вывода: С помощью этого правила можно осуществлять расчет выходных переменных ЭС, например, на основе максиминного произведения: Пусть Прогнозируемые значения выходных переменных (нечеткие значения) определяются в виде соответствующих функций принадлежностей. Конкретные числовые значения выходных параметров Задачей заключительного этапа методики (пункт 9) является проверка адекватности полученной модели. Модель считается адекватной реальной ситуации, если найденные с ее помощью на компьютере характеристики объекта совпадают с заданной степенью точности, реальными данными, полученными экспериментально на практике. Как правило, в качестве критерия адекватности, являющегося мерой соответствия модели реальной ситуации на практике, используется величина рассогласования расчетных (модельных) Выводы. Разработана структура и описаны функциональные блоки экспертной системы для диагностики болезни с применением методов теории нечетких множеств. Показана, что применение методов теории нечетких множеств и нечетких выводов позволяют повысить надежность и адекватность экспертных систем при проведении медицинской диагностики. Предложена процедура оценки в системе расспроса и предварительной диагностики. Формализация взаимосвязи болезни и симптомов проведена на основе построения матрицы нечетких отношений. С применением методов теории нечетких множеств описан алгоритм диагностики болезни. Оригинальность и новизна результатов определяется тем, что предлагаемая система позволяет выполнить комплексные выводы и диагностики с помощью блока нечетких выводов и знаний специалистов–экспертов медицинских учреждений, а также с учетом особенности человеческой процедуры оценки разработан метод проведения экспертной оценки в нечеткой среде. Предлагаемая экспертная система может способствовать раннему обнаружению и лечению болезней благодаря активной постановке диагноза самой системой. С целью повышения точности выводов в предлагаемой системе введена модель, основанная на нечетком соответствии как более широком понятии, и достигнута возможность получения адекватных и гибких выводов. Библиографический список 1. Герман О.В. Введение в теорию экспертных систем и обработку знаний. -Минск: ДизайнПРО, 1995. -256с. References 1. German О.V. Vvedenie v theory exprtnyh system I obrabotku znanii. Minsk DizainPPRO, 1995. -256s. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||

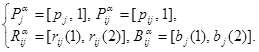 (6)
(6) 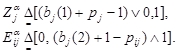 (7)
(7)