Геометрический анализ выбора оптимального номенклатурного состава и объема выпуска продукции при ограничениях на ресурсы
Geometrical analysis of nomenclature of choosing the optimal structure and volume of production under constraints on resourcesУДК 338.512 15.09.2014 Выходные сведения: Авторы: Г.М. Охезина (НГТУ им. Р.Е. Алексеева) Authors: G. M. Ohezina (NSTU n. a. R. E. Alekseev) Ключевые слова: Keyword: Аннотация: Annotation: Под оптимальным понимается такой состав и объем выпуска продукции каждого наименования, который при имеющихся ограничениях на ресурсы позволяет достичь максимальных результатов (максимальной прибыли) или минимальных затрат. В том и другом случае менеджерам предприятий приходится иметь дело с экстремальными задачами, для решения которых используются обычные алгебраические методы, а для более сложных – методы линейного программирования [1]. Однако для того, чтобы лучше показать, из чего складывается процесс выработки принимаемого решения по оптимизации номенклатурного состава и объема выпуска изделий в многоменклатурном производстве при имеющихся ограничениях на ресурсы, исследование данной проблемы проведем с помощью так называемого геометрического анализа. Необходимой предпосылкой нахождения оптимального решения является, во-первых, выбор критерия оптимальности и, во-вторых, установление имеющихся ограничителей ресурсов. Примерами ограничений на ресурсы могут являться: объем производства, когда существуют границы спроса на продукцию, трудовые ресурсы (общее количество или по профессиям); материальные ресурсы (недостаток материалов для изготовления различных видов продукции в необходимых количествах) и др [2, 3, 4, 5]. Представим такую производственную ситуацию. Предприятию необходимо наладить производство из одного и того же материала двух наименований изделий (И1 и И2): при наличии следующих ограничений: расход материальных ресурсов на одно изделие составляет соответственно 7 и 10 кг, трудовых – 16 и 12 чел./часов. Лимит ресурсов на предприятии равен по материальным –
7 х1+10 х2 ≤ 7000; 16 х1+12 х2 ≤ 12000.
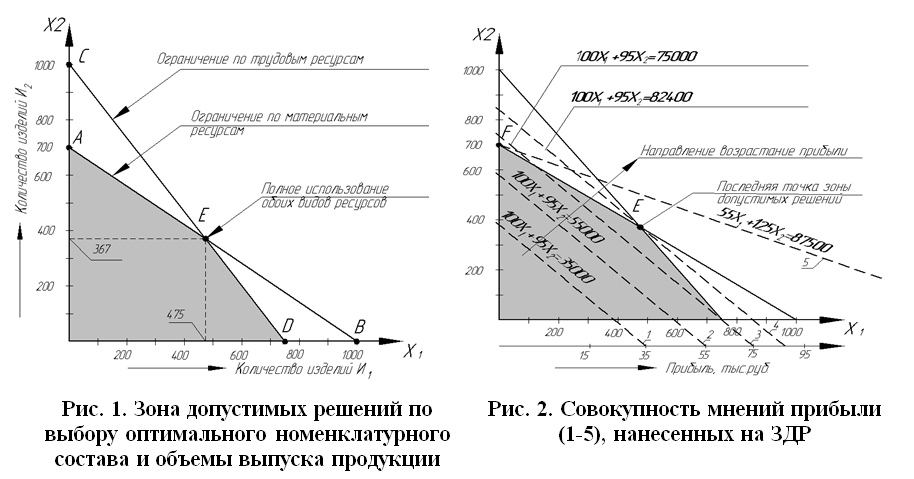
Приведенные неравенства определяют способы использования каждого вида ресурса при различных планах производства изделий. Они выражают тот факт, что использовать материальные и трудовые ресурсы больше, чем это определенно лимитом, невозможно. В результате подстановки в неравенства различных значений Х1 и Х2 можно определить, нарушаются ли ограничения по ресурсам и какую прибыль предприятие может получить при том или ином варианте плана. Пересекающиеся в первом квадранте прямые АВ и CD, построенные по координатам точек, найденным из приведенных уравнений, соответствуют двум ограничениям – по материальным и трудовым ресурсам (рис. 1). Нетрудно убедиться, что любая комбинация значений Х1 и Х2, попадающая на прямую, приводит к стопроцентному использованию того вида ресурса, к которому относится данная прямая. Таким образом, каждая из прямых характеризует полное использование ресурса соответствующего вида. Заметим также, что в данном случае имеется единственная оптимальная комбинация значений Х1 и Х2 (количество выпуска изделий И1 и И2), при которой обеспечивается полное использование данных видов ресурсов. Это точка пересечения прямых – точка Е. Площадь под каждой из двух пересекающихся прямых эквивалентна математическому выражению неравенств, имеющих направленный смысл «меньше, чем (<)». Следовательно, все точки, попавшие в первый квадрант и удовлетворяющие ограничениям, должны находиться в пределах затемненной площади или на ее периметре. Назовем эту площадь зоной допустимых решений (ЗДР). Всякая комбинация Х1 и Х2, представляющая возможный номенклатурный состав и объем продукции, должна принадлежать к ЗДР. Критериям оптимальности принимаемого решения является максимизация прибыли. В нашем случае это выразится уравнением: 100 х1 +95 х2 →max. Этот результат соответствует одной точке ЗДР. Для того чтобы определить, какая из точек будет соответствовать максимальной прибыли, на ЗДР нанесем совокупность линий прибыли (рис. 2). Каждая из параллельных прямых (1-4) представляет собой различные комбинации Х1 и Х2 . Все комбинации, принадлежащие к одной и той же прямой, обеспечивают получение одинаковой прибыли. Рассмотрим, например, линию 2 . Если в управление этой линии поставить любую комбинацию значений Х1 и Х2, соответствующую точке на этой линии в ЗДР, мы получим сумму прибыли для данной комбинации (номенклатурного состава и объема продукции), равную 55 тыс. руб. Для доказательства того, что можно ли получить еще большую прибыль, рассмотрим линию 3, определяющую прибыль размером 75 тыс. руб. Из рисунка видно, что часть этой линии находится вне ЗДР и не может быть использована для принятия оптимального решения ни по составу и объему производства, ни по максимизации прибыли. Но так как некоторые точки, лежащие на данной линии, удовлетворяют ограничениям по материальным и трудовым ресурсам, прибыль в сумме 75 тыс. руб. может быть получена. По мере того как линии прибыли перемещаются вверх и вправо (на рисунке показано стрелкой), размер прибыли увеличивается. В соответствие с этим мы должны выбрать такую прямую из совокупности линий прибыли, которая соприкасаясь с ЗДР, была бы последней в последовательности линий. Эта прямая и будет являться линией максимальной прибыли. В нашем примере линией максимальной прибыли является линия 4, проходящая через точку Е. Объемы производства для каждого из видов изделий в соответствии с этим решением равны Х1 = 475 и Х2 = 368. При этих количествах ни по одному виду ограничений не остается резервов. Максимальная прибыль составит 82,4 тыс. руб. Заметим, что при данных ограничениях на ресурсы можно также обеспечить выпуск 750 изделий И1 или 700 изделий И2, но прибыль для этих решений будет меньше (75 и 66,5 тыс. руб. соответственно). Рассмотрим далее, каким был бы оптимальным номенклатурный состав и объем производства продукции при полном использовании ограниченных ресурсов, если бы изменилась относительная прибыльность входящих в него изделий. Допустим, что прибыль от изделия И1 равна 55 руб., а от изделия И2 равна 125 руб. Результатом такого изделия будет являться, прежде всего, изменение положения линий прибыли (изменение угла их наклона к оси Х1) и в соответствии с этим, изменение принимаемого решения. Если бы для этого варианта на ЗДР нанести линии прибыли, как это делалось выше, то последней прямой, максимизирующей прибыль, являлась бы линия 5, проходящая через точку Е – одну из вершин ЗДР. Оптимальное решение здесь состоит в том, чтобы выпускать 700 единиц изделий И2 и ни одного изделия И1. В особых случаях при проведении геометрического анализа решению задачи могут соответствовать не одна, а две смежные вершины ЗДР, т.е. последняя линия прибыли может совпадать на одном из участников с одной из линий ограничения определенного вида ресурса. Если это имеет место, то все точки на линии прибыли, соединяющей обе вершины (например, точки E и F) также соответствуют оптимальным решениям по номенклатурному составу и объему выпуска продукции, а также максимизации прибыли при ограниченности ресурсов [6, 7]. Библиографический список 1. Иванов А.А. Оптимизация использования ресурсов промышленного предприятия методом линейного программирования // Сборка в машиностроении, приборостроении. 2014. № 9. С. 3-5. 2. Амосов Е.А. Геометрический анализ процесса производства // В сборнике: Современные подходы к трансформации концепций государственного регулирования и управления в социально-экономических системах. Материалы 2-й Международной научно-практической конференции, в 2-х томах. Ответственный редактор Горохов А.А.. Курск, 2013. С. 55-57. 3. Косьмина О.И., Стародубцева Ю.В. Выбор управленческих решений в условиях ограниченности ресурсов // Путь науки. 2014. Т. 1. № 9 (9). С. 83-85. 4. Ридченко А.И. Определение полных затрат производственного комплекса на основе оптимизации портфеля заказов // Наука о человеке: гуманитарные исследования. 2012. № 2 (10). С. 96-101. 5. Тавбулатова З.К. Современная экономическая теория ограниченных ресурсов // Вестник Университета (Государственный университет управления). 2012. № 18. С. 96-102. 6. Булдакова Т.С. Экономико-математические модели задач математического программирования // В сборнике: Новые технологии в науке, образовании, производстве Международный сборник научных трудов по материалам международной научно-практической конференции. Ответственный редактор Горохова Марина Николаевна. 2014. С. 198-202. 7. Подчищаева О.В., Бурова М.С. Максимизация прибыли организации при рыночном изменении цен на ее продукцию // Экономический анализ: теория и практика. 2013. № 21 (324). С. 61-64. References 1. Ivanov A.A. Optimizacija ispol’zovanija resursov promyshlennogo predprijatija metodom linejnogo programmirovanija Sborka v mashinostroenii, priborostroenii. 2014. No 9. P. 3-5. 2. Amosov E.A. Geometricheskij analiz processa proizvodstva V sbornike: Sovremennye podhody k transformacii koncepcij gosudarstvennogo regulirovanija i upravlenija v social’no-jekonomicheskih sistemah. Materialy 2-j Mezhdunarodnoj nauchno-prakticheskoj konferencii, v 2-h tomah. Otvetstvennyj redaktor Gorohov A.A.. Kursk, 2013. P. 55-57. 3. Kos’mina O.I., Starodubceva Ju.V. Vybor upravlencheskih reshenij v uslovijah ogranichennosti resursov Put’ nauki. 2014. T. 1. No 9 (9). P. 83-85. 4. Ridchenko A.I. Opredelenie polnyh zatrat proizvodstvennogo kompleksa na osnove optimizacii portfelja zakazov Nauka o cheloveke: gumanitarnye issledovanija. 2012. No 2 (10). P. 96-101. 5. Tavbulatova Z.K. Sovremennaja jekonomicheskaja teorija ogranichennyh resursov Vestnik Universiteta (Gosudarstvennyj universitet upravlenija). 2012. No 18. P. 96-102. 6. Buldakova T.P. Jekonomiko-matematicheskie modeli zadach matematicheskogo programmirovanija V sbornike: Novye tehnologii v nauke, obrazovanii, proizvodstve Mezhdunarodnyj sbornik nauchnyh trudov po materialam mezhdunarodnoj nauchno-prakticheskoj konferencii. Otvetstvennyj redaktor Gorohova Marina Nikolaevna. 2014. P. 198-202. 7. Podchishhaeva O.V., Burova M.P. Maksimizacija pribyli organizacii pri rynochnom izmenenii cen na ee produkciju Jekonomicheskij analiz: teorija i praktika. 2013. No 21 (324). P. 61-64. |